Forces when walking or running. Physics in walking and running.
Forces when walking or running
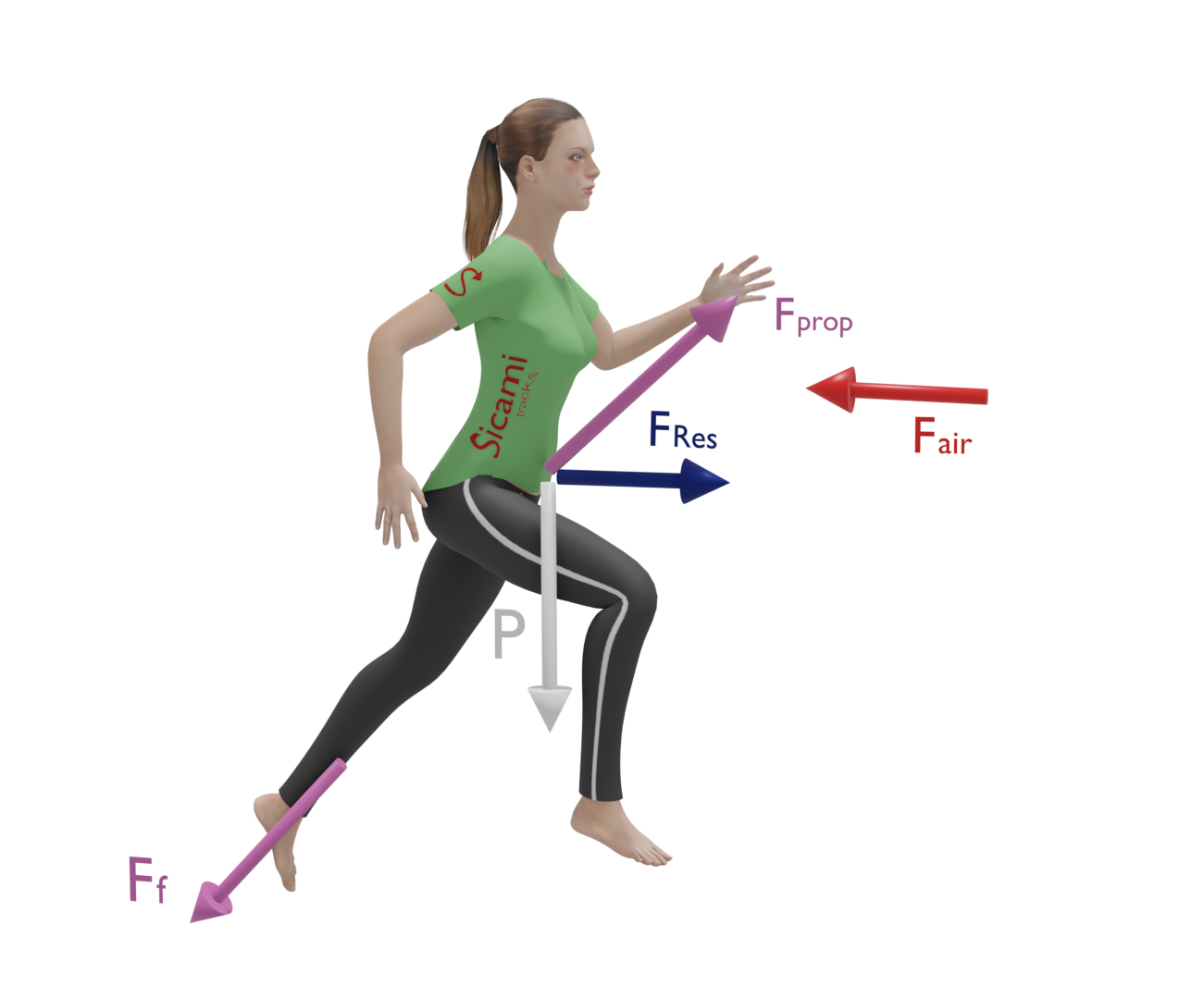
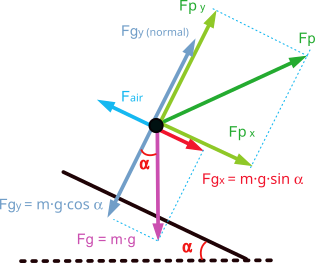
When running or walking there are many forces at work, the most important of which, for the purpose of producing displacement, is the propulsive force exerted by the foot on the ground.
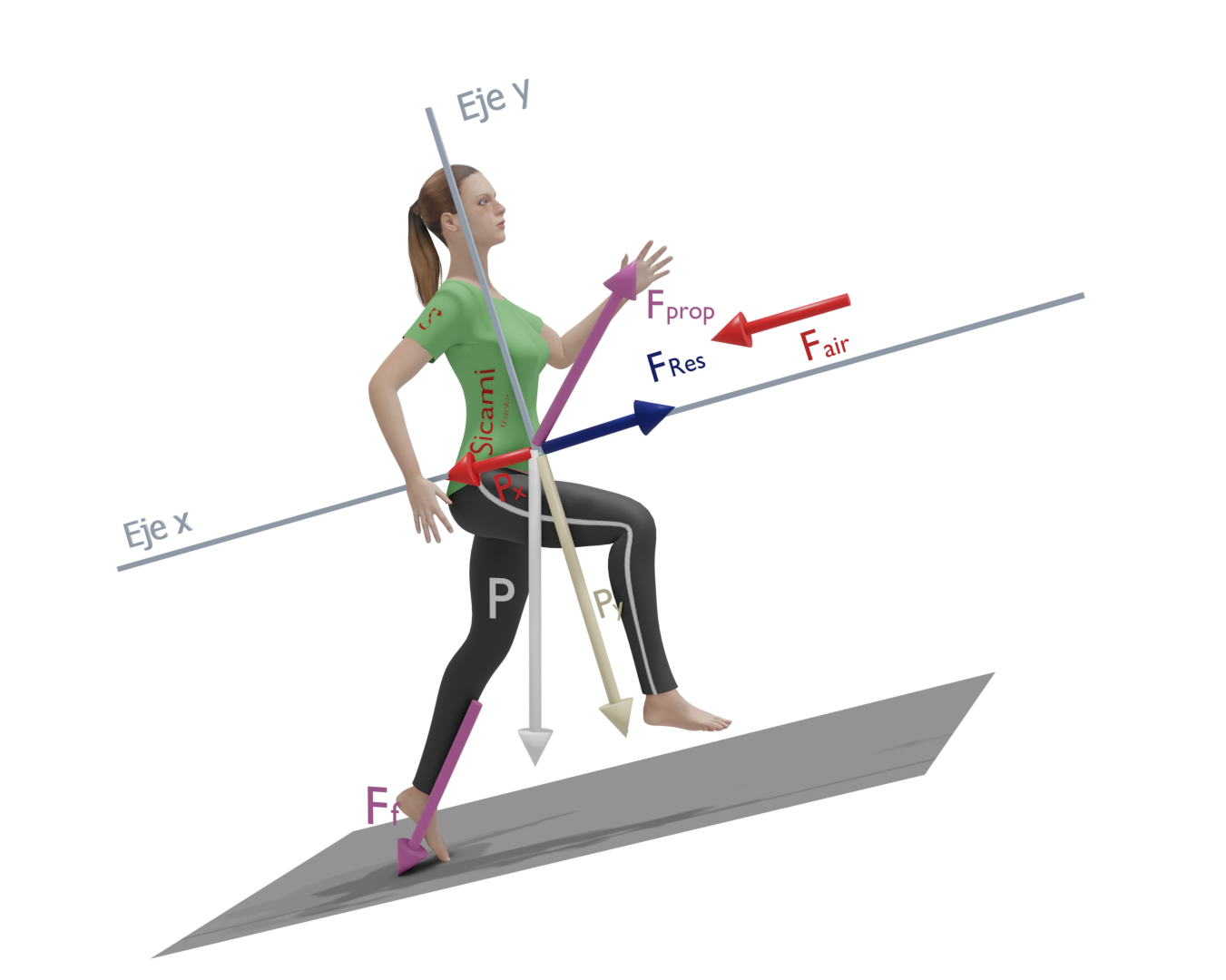
This force has an inclined direction, depending on the angle of the foot strike, and can be broken down into two components in the forward direction, ‘x’, and perpendicular to the ground, ‘y’.
The ‘x’ component is the one that will allow the runner or walker to move forward causing an acceleration in the forward direction. This component will be horizontal when moving on flat ground.
The ‘y’ component is what will allow the runner to overcome gravity and move upwards causing a force in a direction perpendicular to the ground.
Essentially running consists of consecutive parabolic movements in which the runner pushes off the ground to reach a certain maximum height and lands again some distance in front. Consequently, his movement can be divided into two movements, a jumping movement and a forward movement, and the final result will be the consequence of overcoming the different forces that will oppose these movements.

The propulsive force is obtained by applying force with the foot on the ground, with which there must be sufficient frictional force. The ground reaction force (Newton's third law) provides the necessary propulsion. In other words, when we run we exert a force opposite to the direction of motion and according to Newton's third law, the ground exerts a force on us equal and opposite to our force on the ground, which allows forward motion.
If there were no frictional force, it would be impossible to move, just imagine what happens when you try to run on a frictionless surface (e.g. ice). If there were no static friction, the foot would push backwards on the surface and simply slide backwards.
Let's take a closer look at some particular cases.
Running on the flat
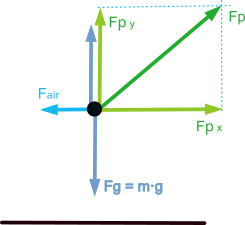
In this case, the main forces opposing displacement are the gravitational force, caused by our own weight, and the aerodynamic drag force caused by the air.
For the forward movement on the flat, the runner must apply a force on the ground that is greater than the sum of the force of gravity and the aerodynamic drag force.
In a simplified scheme it would look like the following figure, where the propulsion force ‘Fp’ has been broken down into a vertical component ‘Fpy’ that must overcome the force of gravity and a horizontal component ‘Fpx’ that must overcome the aerodynamic drag and provide the acceleration.
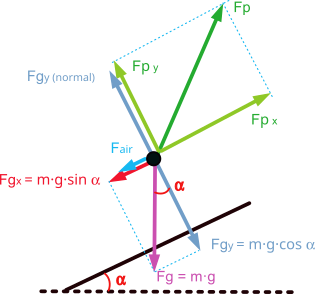
Running uphill
In this scenario an ‘x’ component of the gravitational force appears in the direction of the displacement and in the opposite direction to it. On the other hand, we will observe a reduction in the value of the frictional force.
Although the y-component (perpendicular to the ground) of the gravitational force decreases with the slope of the terrain, it is not sufficient to compensate for the increase in the x-component and the loss of friction with the ground.
Therefore, the force to be applied must be greater than the sum of the force of gravity at ‘x’, the force of gravity at ‘y’ and the aerodynamic drag force.
From an energy point of view, the upward stroke not only involves a change in kinetic energy, but also a net increase in potential energy.
In a simplified scheme it would be as shown in the following figure, where the propulsion force ‘Fp’ has been broken down into a component perpendicular to the ground ‘Fpy’ that must overcome the force of gravity and another one parallel to the ground ‘Fpx’ that must overcome the aerodynamic drag, the ‘x’ component of the gravitational force and, in addition, provide the acceleration.
Running downhill
In this case the ‘x’ component of the gravity force will be favourable to the displacement and the forces to be overcome will be the ‘y’ component of gravity and the aerodynamic drag force.
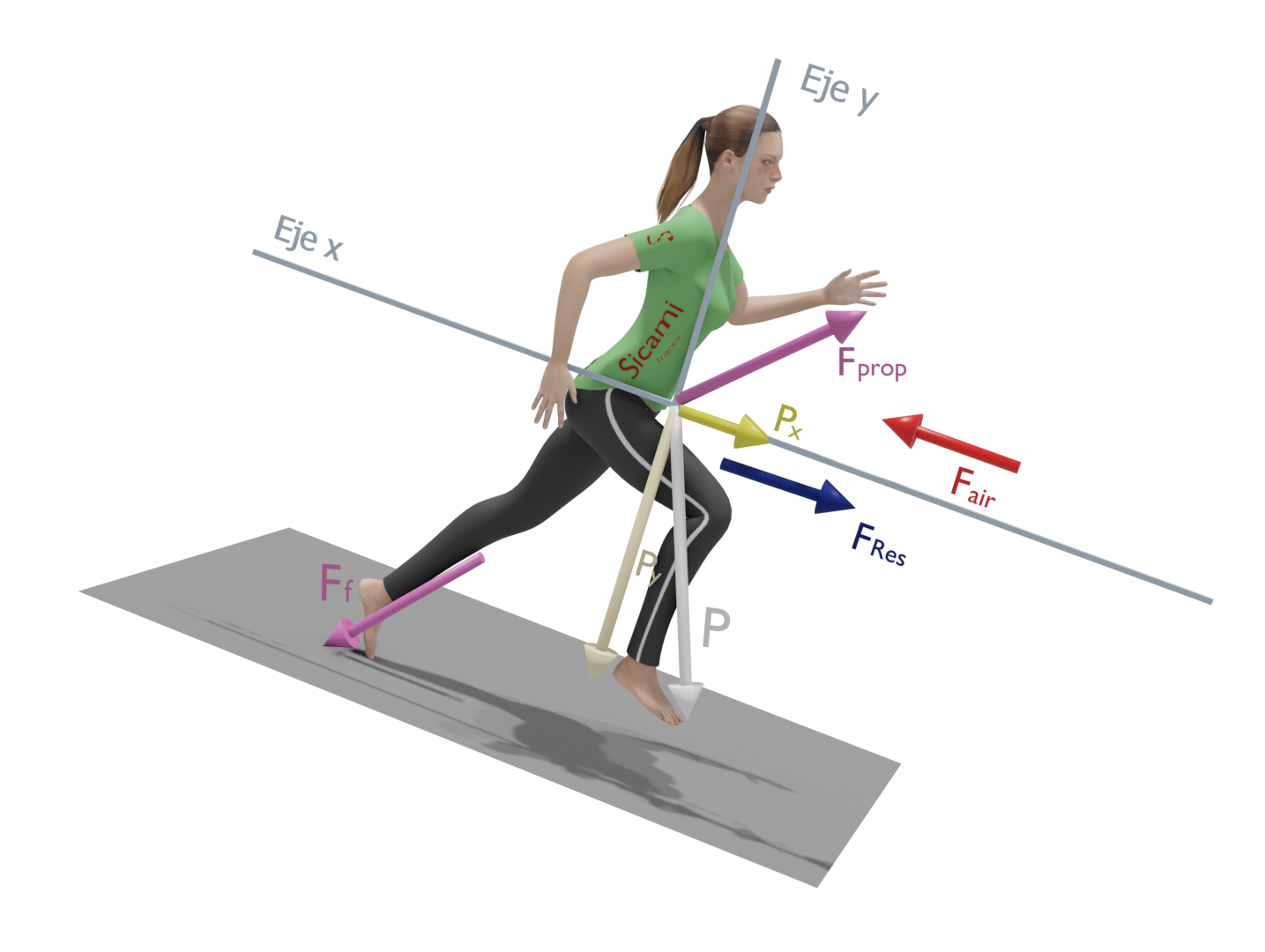
In a simplified scheme it would be as shown in the following figure, where the propulsive force ‘Fp’ has been broken down into a component perpendicular to the ground ‘Fpy’ and another parallel to the ground ‘Fpx’ that must overcome the aerodynamic drag in addition to providing the acceleration.
The ‘x’ component of the gravitational force has the same direction and sense as the displacement, so the effort to move forward will be less in this case.
Sicami Tracks - Start