Coordinate reference systems. Datum. Basic concepts.
Coordinate reference systems. Datum. Basic concepts
The Datum is a geodetic reference system consisting of an ellipsoid, on which a coordinate system has been established to allow the location of any point on its surface and its position in relation to the Earth.
Fundamental point
In order to establish this coordinate reference system it is necessary to previously establish a clear relationship between the relative positions between the ellipsoid and the geoid so that the ellipsoid fits as well as possible to the region where it will be used. For this it is necessary to define a point common to both, where both coincide and which will be a tangent point to the ellipsoid and the geoid. This point is called "fundamental point". The fundamental point will be defined by its geographical coordinates of longitude and latitude.
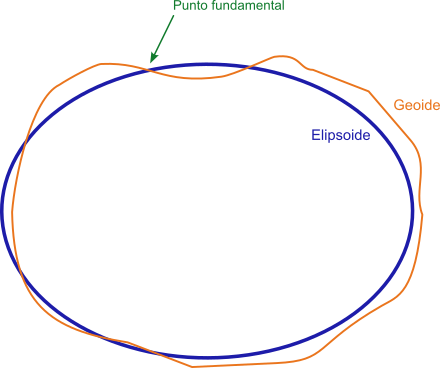
At present, satellite systems have made it possible to develop global datums, where the origin of coordinates is usually established at the center of mass of the Earth.
Local or regional Datums and global Datums
Therefore, we can distinguish between local or regional datums and global datums.
Local datums
Local datums define an origin and location of a coordinate system valid for a certain area of the Earth, although not for all of it, and consists of the ellipsoid defined by its axes and flattening index and by its "fundamental point".Global datums
In the global Datums the geometric center of the ellipsoid usually coincides with the center of mass of the Earth and there is no "fundamental point" as such.An example of a local datum would be the European datum ED 50 that uses the Hayford Ellipsoid with semi-major axis a = 6,378,388 meters and flattening f = 1 / 297. Its origin for longitudes is the Greenwich meridian and its Fundamental Point is located in Potsdam (Germany) at coordinates 52º22'51.446 "N 13º03'58.741 "E.
As an example of global datum we would have the WGS84 that uses the GRS_1980 Ellipsoid with semi-major axis a = 6.378.137 meters and flattening f = 1 / 298,25722356300003. Its longitude origin is the Greenwich meridian and it has no fundamental point as it is global.
Datum WGS84
The GPS systems use internally the WGS84 Datum so it is convenient to configure the Datum of the device according to the cartography that we are using. The device will be in charge of making the appropriate conversions so that the coordinates of each point coincide on the map. In the same way, the tracks in GPX format that are generated by a GPS device will always store the coordinates according to the WGS84 Datum.
Vertical Datums
As in the case of the Datum for horizontal coordinates, in the case of vertical coordinate systems a vertical Datum is established which will be the surface to be taken as a reference with zero elevation or altitude. In practice, normally data from measurements and calculations stored in elevation raster files will be used.Orthometric altitude and ellipsoidal altitude
The two surfaces to be used will be the ellipsoid and the geoid which gives rise to two definitions of altitude or height:
Orthometric altitude or orthometric height: When the reference surface is the geoid, equivalent to the altitude above mean sea level. The orthometric height will be the distance between the point on the ground and the geoid in the direction of gravity or "plumb line". This distance can be positive or negative depending on whether the point is above or below the surface of the reference geoid. They are commonly used for topographic mapping.
Ellipsoidal altitude or Ellipsoidal height: When the reference surface is the ellipsoid. The ellipsoidal height will be the distance between the point on the ground and a line perpendicular to the ellipsoid. This distance can be positive or negative depending on whether the point is above or below the surface of the reference ellipsoid. This model is the one used by GPS systems.
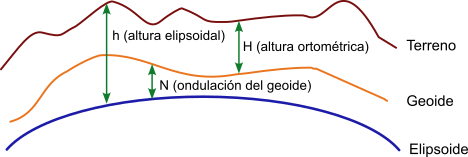
Relationship between orthometric and ellipsoidal altitude
If data on the geoid undulation in a certain area are available, it is possible to obtain the approximate orthometric height from the ellipsoidal height by applying the following relation:
Undulation of the geoid = ellipsoidal height - orthometric height,
N = h - H
from where:
Orthometric height = ellipsoidal height - geoid undulation,
H = h - N
Sicami Tracks - Start