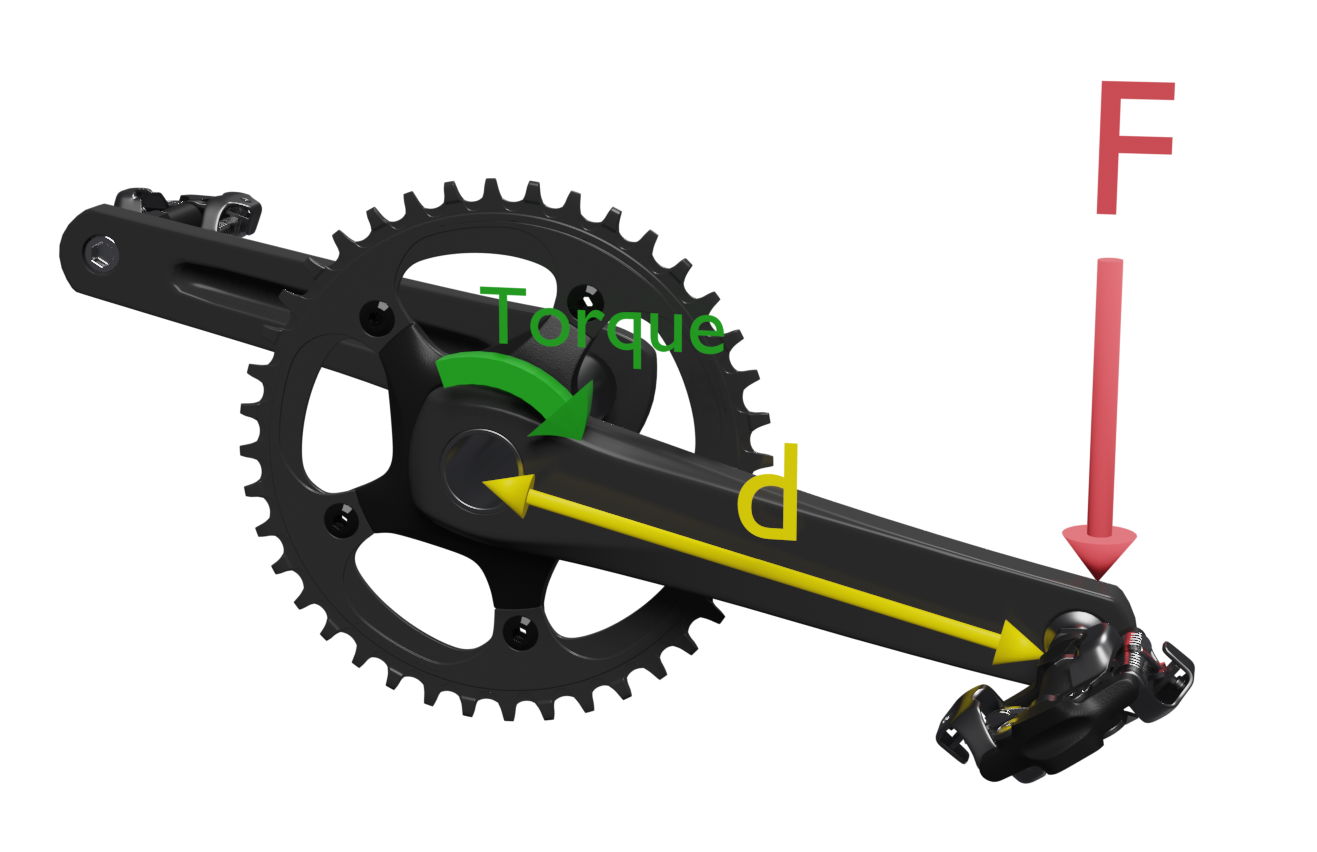
Forces on the pedal. Torque.
Torque of force on the pedal
When pedaling our force is applied to the pedal and transmitted to the axle through the crank, which acts as a lever. The application of the force will cause a rotation with which we will observe a "torque" or "torque".We can define torque as the ability of a force to rotate an object when applied to it.
The value of the torque of a force can be calculated as the product of the value of the force applied at a point, multiplied by the distance from that point to the torque axis. Its unit is the newton per meter.
T = F · d
F = force on the pedald = distance to the center of rotation (distance pedal axis - crank axis)
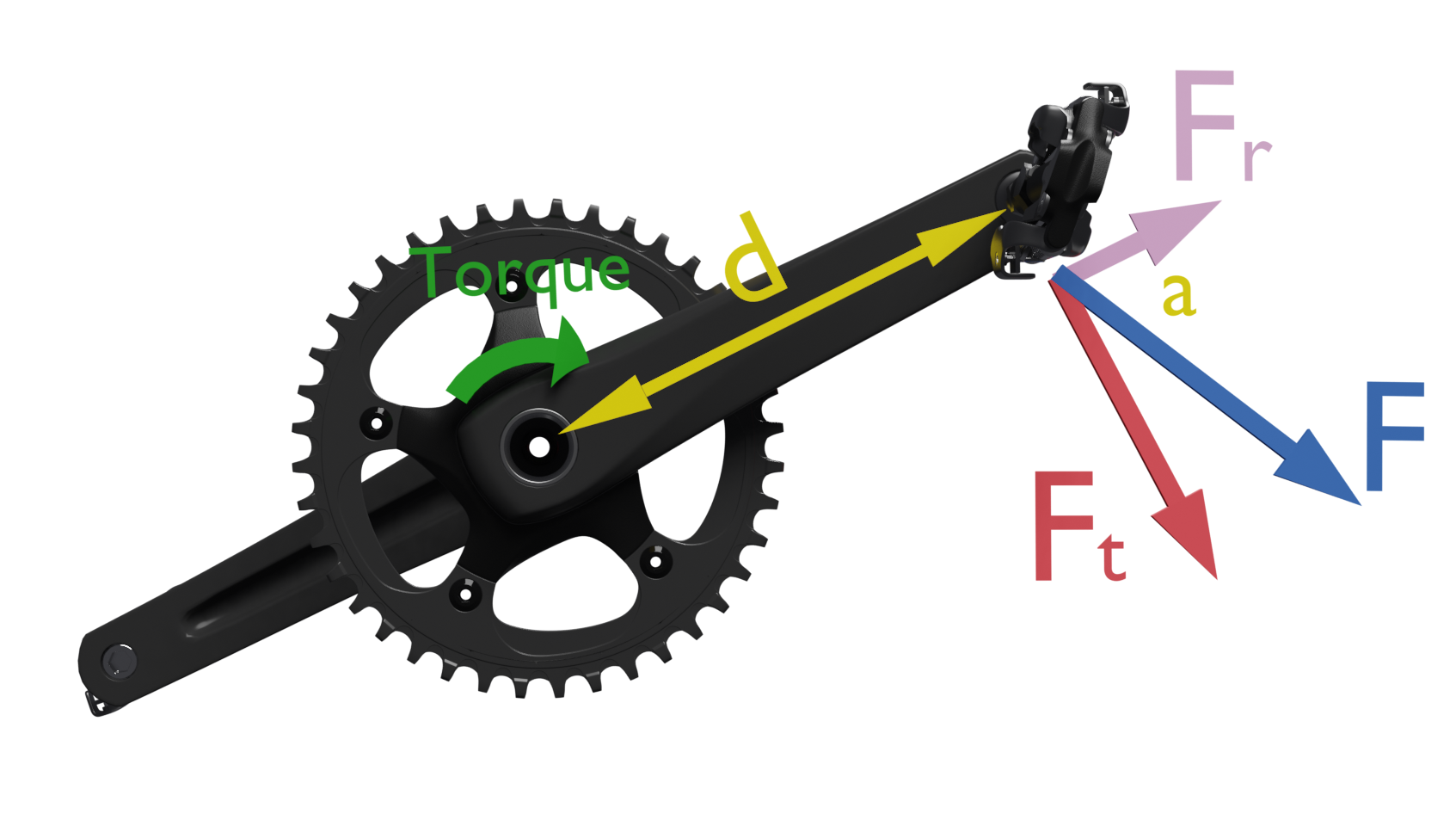
Tangential and radial components of pedal force
But this would only be valid for forces applied perpendicular to the distance. Since the force can be applied at different angles, depending on the thrust position, we will extend the formula as follows:
T = F · d · sen (a)
Where a is the angle of application of the force with respect to the line joining the point of application and the center of rotation. The angle whose value is less than 90º will always be taken. This is equivalent to decomposing the force exerted on the pedal into two components:
• a tangential component Ft, which is tangent to the circumference drawn by the pedal Ft = F sin (a)• a radial component, Fr in the direction of the connecting rod. Fr = F cos (a)
The tangential component will always be perpendicular to the connecting rod and is the one that produces useful torque. The radial component Fr will only compress or stretch the connecting rod.
Pedalling efficiency and effectiveness
Assuming that we pedal pushing down vertically, if the crank is also in a vertical position at "12-6 o'clock", the Ft component perpendicular to the distance line will be zero and the applied force will not cause any rotation.

Mathematically: T = F · sin (0) = F · 0 = 0

Mathematically: T = F · sen (90) = F · 1 = F
From all of the above we can conclude that the greatest efficiency in pedaling would be obtained by applying the force on our pedals always describing the tangential direction (perpendicular to the crank) which would generate 100% efficient torque, although this seems physiologically complex and would require control of the motricity of both legs beyond the reach of a standard human being.
Sicami Tracks - Home