Cartographic projections
Carthographic projections
A map is a two-dimensional representation of the earth, which has three dimensions, the transition from a three-dimensional representation to two dimensions is known as a projection.
In order for there to be a correspondence between the points on the curved surface of the earth and those on the flat surface of a map, a grid is used with x and y coordinates obtained from the longitude and latitude coordinates through different mathematical calculations. This causes that there is inevitably a deformation when making the projection, so it will be depending on what parameters we want to read (distances, surfaces or angles) that one or another of the available projection systems will be used, making a projection that correctly represents impossible. all three simultaneously.
Based on this we can distinguish three types of projection
Projections according to conservation of distances, surfaces or angles
Equidistant projection:
where distances are preserved
Equivalent projection:
where surfaces are kept
Conformal projection:
where the shape or relationship of angles between points is preserved.
To improve the result of the projections, geometric surfaces can be used that will later be lowered in the plane. Let's see some of the most common:
Projections on geometric surfaces
Cylindrical projection.
It is obtained by placing a tangent cylinder to the terrestrial sphere at Ecuador. The Mercator projection is the best known cylindrical projection. The meridians and parallels will be perpendicular in the projection, the distance between the parallels will increase as the latitude increases. This will produce a larger deformation the further away the north or south position is from the Equator. The Equator will be the only line where the scale will be preserved. The territories and countries located further north will appear larger than life and the poles are not represented as they would be at infinity. Although this system causes the areas near the poles to be greatly distorted, it is useful for navigation since it is a type of "conformal" projection, that is, it preserves the angular relationship between points.
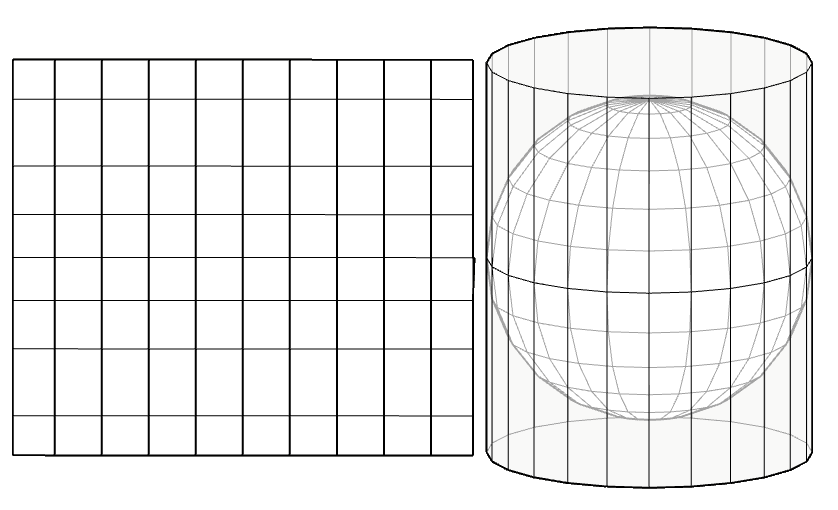
The Transverse Mercator projection
The Transverse Mercator projection is a variant of the Mercator projection where the meridians are expanded to the east or west of the Greenwich meridian. The meridians are represented by curved lines parallel to each other and convex towards the equator. In this case, the distortions are greater the further away the position is from the Greenwich meridian and this will be the only line where the scale will be preserved.
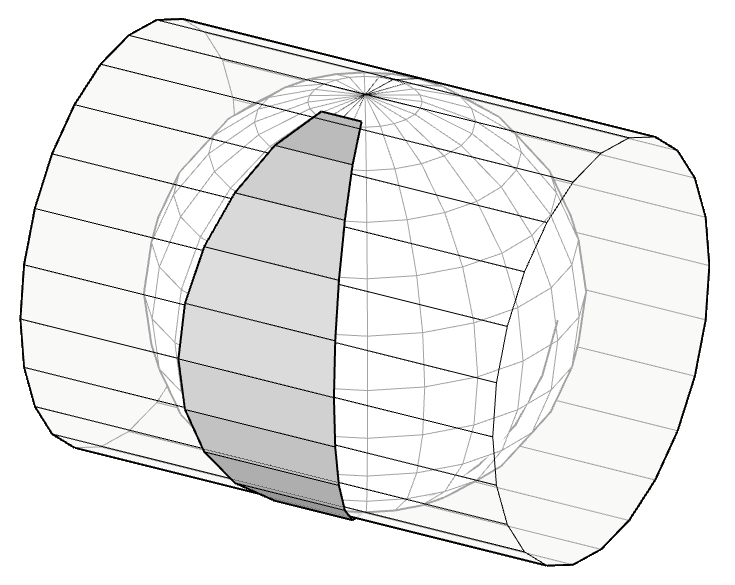
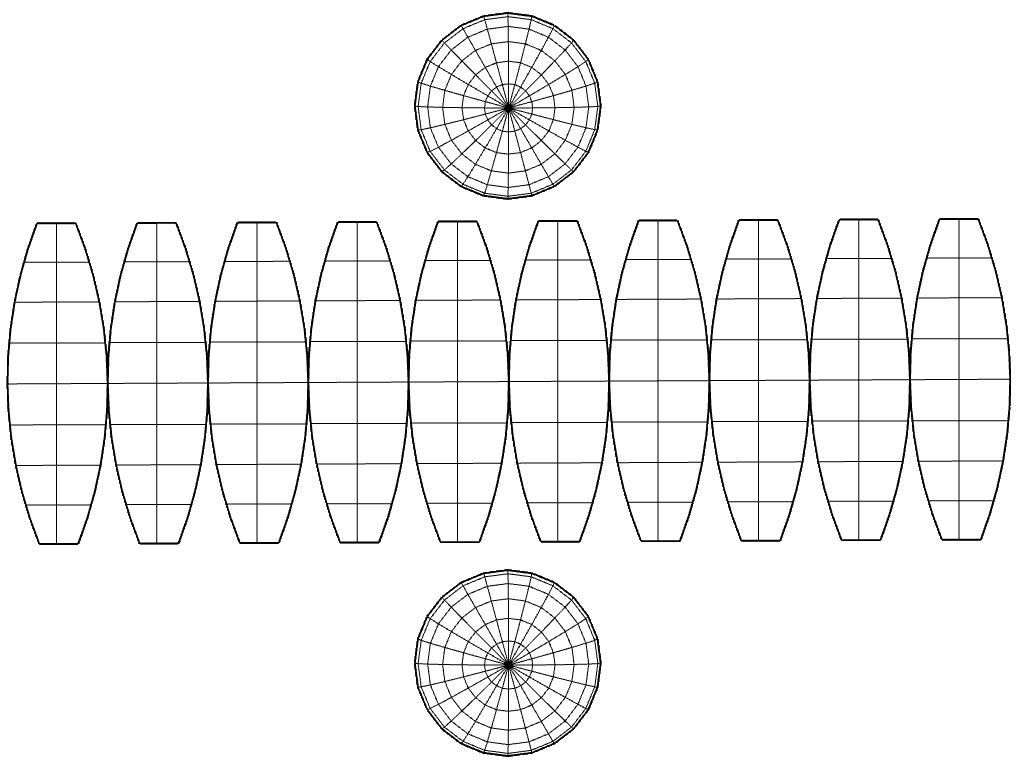
The Universal Transverse Mercator Projection (U.T.M.)
The Universal Transverse Mercator Projection (U.T.M.) is another projection system, based on the transverse projection, which divides the globe into 60 sectors or zones along the Equator (each sector covers 6 degrees of longitude). Each zone has a central meridian and the intersection of this central meridian with the Equator is established as the "x" and "y" origin of the zone.
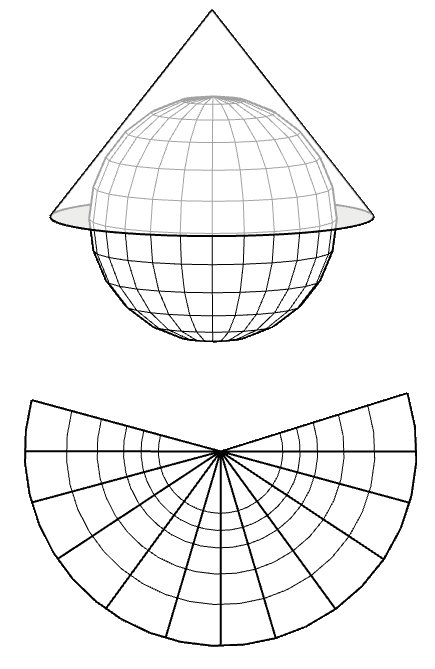
Conical projection
Meridians and parallels are projected onto a conical surface tangent to the vertex of the cone on the axis formed by the poles. The meridians will become straight lines starting from the pole and the parallels will become concentric circles centered on the poles.
Sicami Tracks - Home