Coordinate reference systems. Ellipsoid and geoid.
Coordinate reference systems. Ellipsoid and geoid. Basic concepts
For the representation of a geographic data, it is necessary to have a spatial reference that positions it on the surface of the Earth, that is, a coordinate reference system. These geographic data are currently in the form of digital files, according to two models, the vector model, which is composed of points, lines and polygons, and the raster model, which consists of cells of a matrix or grid.
The vector model is appropriate for discrete objects or phenomena with clear boundaries (parcels, buildings, cadastre, etc.), while the raster or matrix structure model, by allowing each unit of the matrix to be assigned a different value, is more appropriate for quantitative variables, such as temperatures, rainfall, etc. that vary according to x and y position, as well as in the vertical position.
Whatever the model, it must incorporate a reference system of both horizontal and vertical coordinates, indicating the vertical position with respect to some reference system.
Earth's shape, the ellipsoid.
The shape of the earth is approximately spherical. Although it is generally accepted that the regular geometric shape that best fits the real shape is the ellipsoid of revolution.
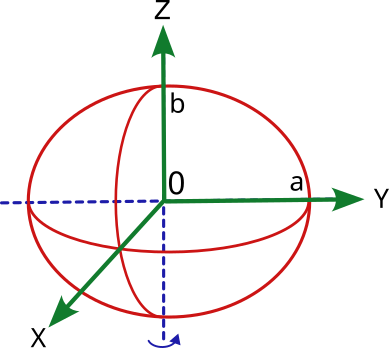
An ellipsoid of revolution is generated when an ellipse is rotated in space around one of its axes. The ellipse is defined by two axes, one horizontal "a", the other vertical "b" and a flattening index "f" being: f = (a-b)/a
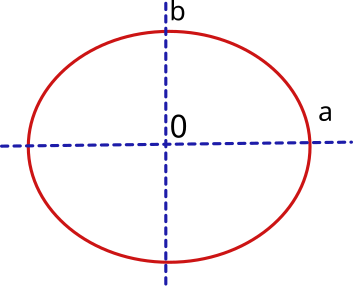
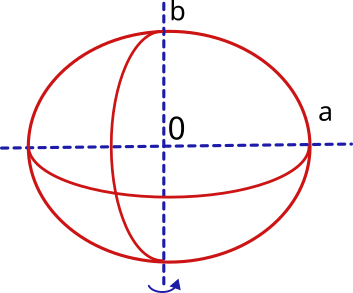
Therefore, to define the terrestrial ellipsoid it will be necessary to know its semi-major axis, which will correspond to the equatorial radius (at the equator) and its semi-minor axis, which will correspond to the polar radius (from center to north and south poles). In addition, it will be necessary to know the flattening index.
The ellipsoid model will serve as the basis for the horizontal coordinate reference systems.
Shape of the Earth, the geoid
But from the geometrical point of view, the real shape of the Earth is not regular. Neither is the distribution of masses and materials in its interior. If we take as a reference the gravimetric potential of each point of the surface, we will obtain an irregular figure called geoid.
The geoid is a theoretical surface of equal potential (equipotential) of the earth's gravity field, which coincides approximately with the mean sea level and which joins all points that have the same gravity potential, i.e. that are attracted with the same gravitational intensity towards the center of the earth. The starting point is the mean ocean level and different techniques are used to obtain values of equal gravimetric potential in the emerged zones.

Relationship between ellipsoid and geoid. Ellipsoidal height, orthometric height and geoidal undulation
To define the geoid, its surface is compared with that of the regular ellipsoid, obtaining the difference for each point of the Earth. This information is usually stored in raster files.
The difference in height at any point between the height of the ellipsoid and the height of the geoid is known as the orthometric height and the variation between the geoid and the ellipsoid is known as the geoidal undulation.
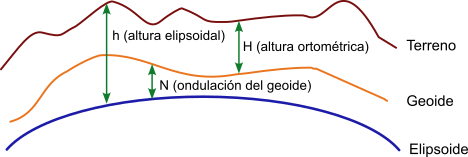
h = vertical distance between the terrain point and the ellipsoid or ellipsoidal height
H = vertical distance between terrain point and the geoid or orthometric height
N = vertical distance between the geoid and the ellipsoid or geoidal undulation
If we said earlier that the ellipsoid would be the basis for the horizontal coordinate reference systems, the Geoid will be the basis for the vertical coordinate reference systems.
The positions calculated by GPS devices are of ellipsoidal type and the associated reference system, known as World Geodetic System WGS, refers to a global reference ellipsoid that was first established in 1960 and has been improved on subsequent occasions, the current version being WGS84, defined in 1984.
Recommended article: Horizontal and vertical coordinate systems. Datum
Sicami Tracks - Home