Fuerzas sobre el pedal. Momento de torsión o torque.

Momento de torsión o torque de la fuerza sobre el pedal

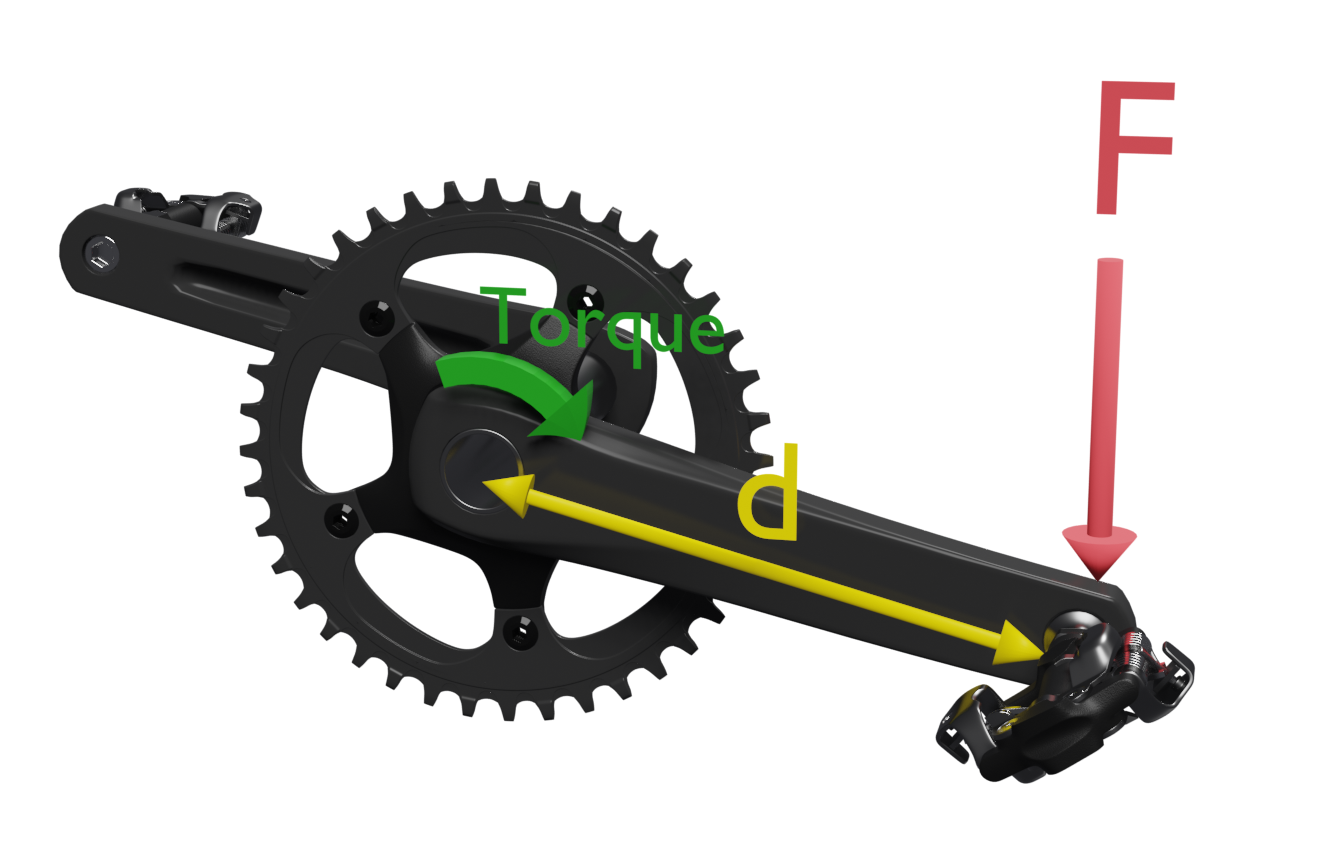
Al pedalear nuestra fuerza se aplica sobre el pedal y se transmite al eje a través de la biela, que actúa a modo de palanca. La aplicación de la fuerza provocará un giro con lo que observaremos un “momento de torsión” o “torque”.

Podemos definir el momento de torsión como la capacidad una fuerza de hacer girar un objeto al aplicarla sobre él.

El valor del momento de torsión de una fuerza se puede calcular como el producto del valor de la fuerza aplicada en un punto, multiplicada por la distancia de ese punto al eje de torsión. Su unidad es el newton por metro.

T = F · d

F = Fuerza sobre el pedal

d = distancia al centro de giro (distancia eje pedal – eje biela)

Componentes tangencial y radial de la fuerza de pedaleo

Pero esto solo sería válido para fuerzas que se apliquen perpendicularmente a la distancia. Cómo la fuerza puede aplicarse en diferentes ángulos, dependiendo de la posición de empuje, ampliaremos la fórmula como sigue:

T = F · d · sen (a)

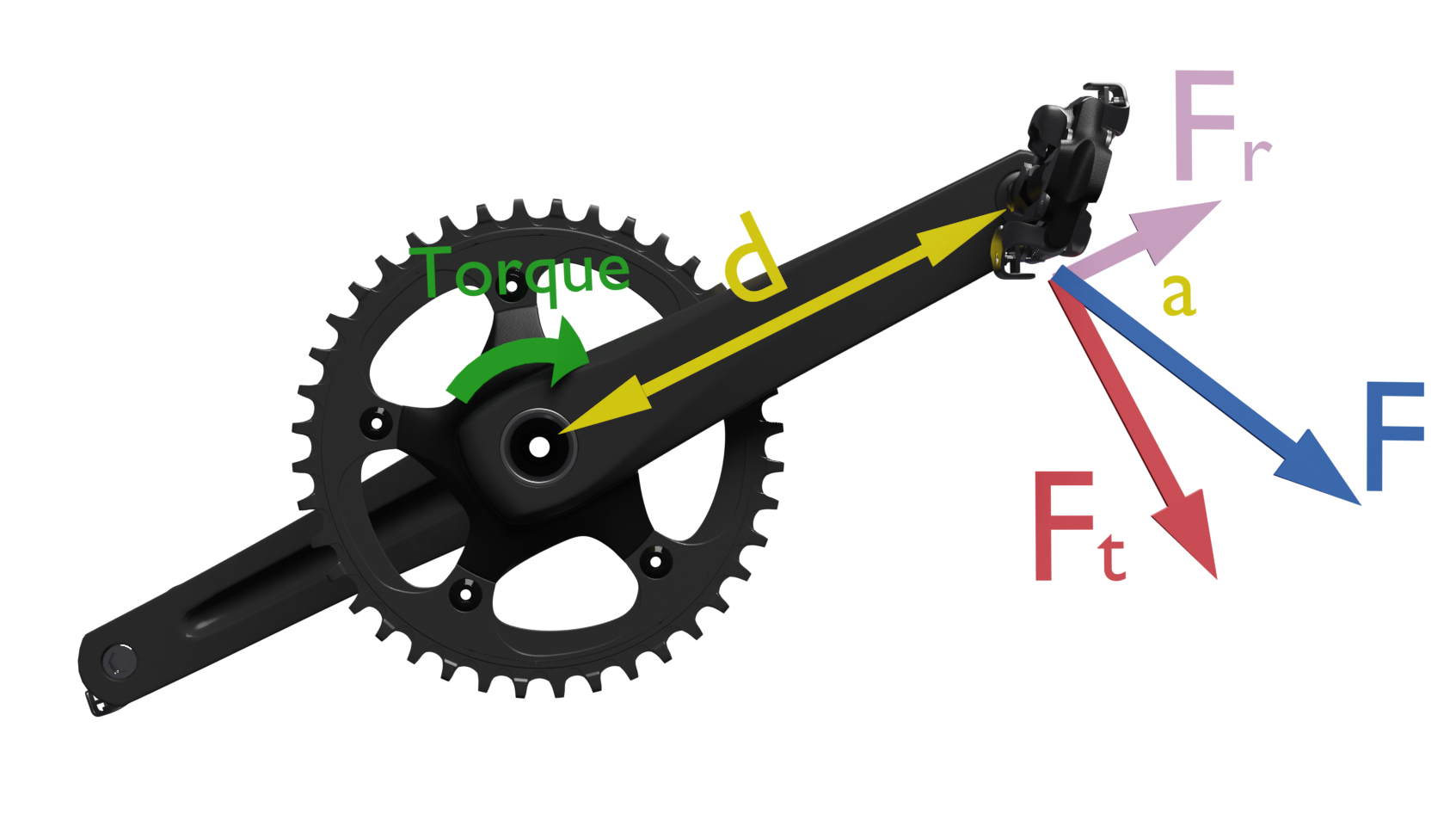
Donde a es el ángulo de aplicación de la fuerza respecto a la línea que une el punto de aplicación y el centro de giro. Siempre se tomará el ángulo cuyo valor sea menor de 90º. Esto es equivalente a descomponer la fuerza ejercida sobre el pedal en dos componentes:

• una componente tangencial Ft, que es tangente a la circunferencia que dibuja el pedal Ft = F sen (a)

• una componente radial, Fr en la dirección de la biela. Fr = F cos (a)

La componente tangencial siempre será perpendicular a la biela y es la que produce momento de torsión útil. La componente radial Fr solo comprimirá o estirará la biela.

Eficacia y eficiencia del pedaleo

La fuerza “útil” dependerá por tanto del ángulo de aplicación de la fuerza sobre el pedal y este a su vez depende fundamentalmente de la posición de las bielas.

Suponiendo que pedaleamos empujando hacia abajo verticalmente, si la biela se encuentra también en posición vertical a las “12-6”, la componente Ft perpendicular a la línea de la distancia será nula y la fuerza aplicada no provocará ningún giro.

Matemáticamente:   T = F · sen (0) = F · 0 = 0

 

En el otro extremo, si la biela se encuentra en posición horizontal a las “3-9”, la componente Ft perpendicular coincidirá completamente con F y toda la fuerza aplicada provocará momento de torsión y por tanto giro.

Matemáticamente:   T = F · sen (90) = F · 1 = F

 

De todo lo anterior podemos concluir que la mayor eficiencia en el pedaleo se obtendría aplicando la fuerza sobre nuestros pedales describiendo siempre la dirección tangencial (perpendicular a la biela) lo que permitiría generar momento de torsión eficiente al 100%, aunque esto se antoja fisiológicamente complejo y requeriría de un control de la motricidad de ambas piernas fuera del alcance de un ser humano estandar.