Articulos relacionados con "Informacíón técnica y curiosidades"
Citocromo P450 como biomarcador de contaminación en aves
El citocromo P450 y los contaminantes ambientales
Durante la evolución, los animales, plantas y protistas han desarrollado una serie de mecanismos para la defensa contra los xenobióticos (drogas, pesticidas, anestésicos…) que acceden al organismo. Entre ellos se encuentra el sistema metabolizante del citocromo P450 (CYP450), una enorme y diversa superfamilia de hemoproteínas.
Su nombre proviene del hecho que estas son proteínas celulares (cito) coloreadas (cromo) que tras ser reducidas por NADPH, son capaces de unirse al CO y absorber luz a una longitud de onda de 450 nanómetros con su pigmento.
La mayor concentración de enzimas CYP involucradas en la biotransformación de xenobióticos se encuentra en el hígado –y en el retículo endoplasmático de los organismos eucariotas– pero están presentes en prácticamente todos los tejidos.
Presentan una amplia versatilidad funcional: es capaz de catalizar una gran cantidad de procesos y unirse a un número elevado de sustratos, aunque realiza principalmente reacciones de oxidación. Esto hace que el citocromo P450 sea un elemento clave para entender la respuesta a un proceso biológico, a un estado patogénico, de respuesta a un tratamiento farmacológico o a la contaminación.
En las últimas décadas se ha comprobado que los compuestos organoclorados, los bifenilos policlorados PCB y el pesticida DDT son de gran preocupación como contaminantes ambientales, los cuales pueden inducir el sistema CYP. Muchos hidrocarburos se unen a receptores específicos y desencadenan una serie de señales que resultan en la inducción de la expresión de CYP1A, una isoforma de P450 involucrada en la respuesta oxidativa a contaminantes.
Las aves en los Grandes Lagos
Un ejemplo del efecto de estos compuestos es el caso de las aves en los Grandes Lagos.
Además de la disminución de la población, se observaron deformidades en el pico, las patas, la cabeza y los ojos en los depredadores superiores, como las águilas calvas, las águilas pescadoras o las aves acuáticas coloniales, en tasas elevadas en comparación con las poblaciones de áreas más remotas.
Ante esto, se había planteado la hipótesis de la toxicidad de los compuestos similares a las dioxinas (DLC). Los resultados de la exposición a los DLC fueron signos de síndrome de desgaste, activación de enzimas oxidativas hepáticas, supresión inmunitaria y anomalías del desarrollo. Estos datos llevaron a mejores herramientas para evaluar tanto la toxicidad de las DLC como la exposición a estas. Por ejemplo, la capacidad de las DLC para inducir la actividad de CYP1A in vitro para evaluar la sensibilidad de una especie en particular. (Tillitt & Society of Environmental Toxicology and Chemistry, 2013)
Este ejemplo es solo uno de los muchos casos en los que el citocromo P450 ha ayudado como biomarcador a determinar el impacto de compuestos contaminantes tanto en el entorno como en los mismos organismos que conviven en él, y con ello al desarrollo de estrategias y métodos para combatir y prevenir el deterioro de los ecosistemas.
Cómo conectar, vincular o integrar Oruxmaps con Sicami o Strava para transferir o exportar tracks y rutas automáticamente. Guía paso a paso con imágenes.

Este procedimiento afectará a todas las nuevas rutas grabadas, pero no a las ya existentes que habrá que transferir manualmente. El procedimiento manual se indica al más adelante en este artículo
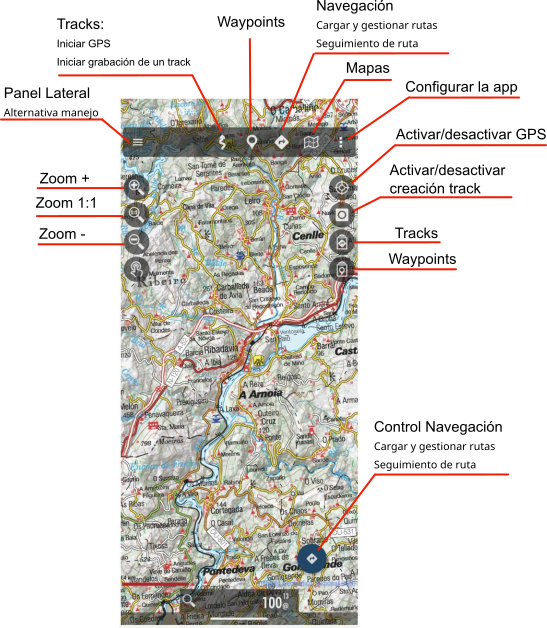
Esquema de la pantalla principal Oruxmaps con los elementos más destacados.
Ir a Configuración --> Integraciones --> Subir Automáticamente --> Marcar Sicami o Strava
Es imprescindible tener configuradas las cuentas correspondientes, si no lo estuvieran se solicitarán los datos o se indicará mediante un mensaje.
El procedimiento paso a paso sería el siguiente:
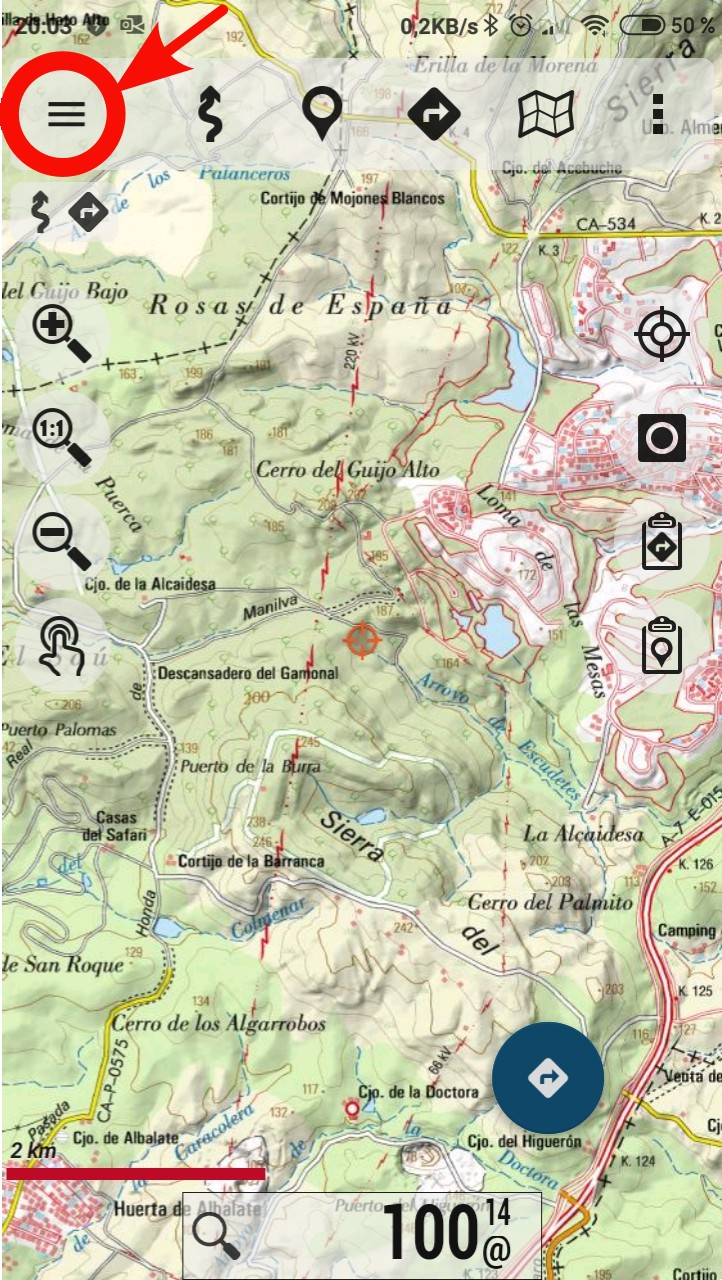
Pulsar sobre el icono del "Panel Lateral", (tres líneas horizontales en la zona superior izquierda). Esta opción también es accesible desde "Configurar la app" (icono con tres puntos en la zona superior derecha).
Acceder a "Configuración global" pulsando sobre el icono de rueda de configuraciones
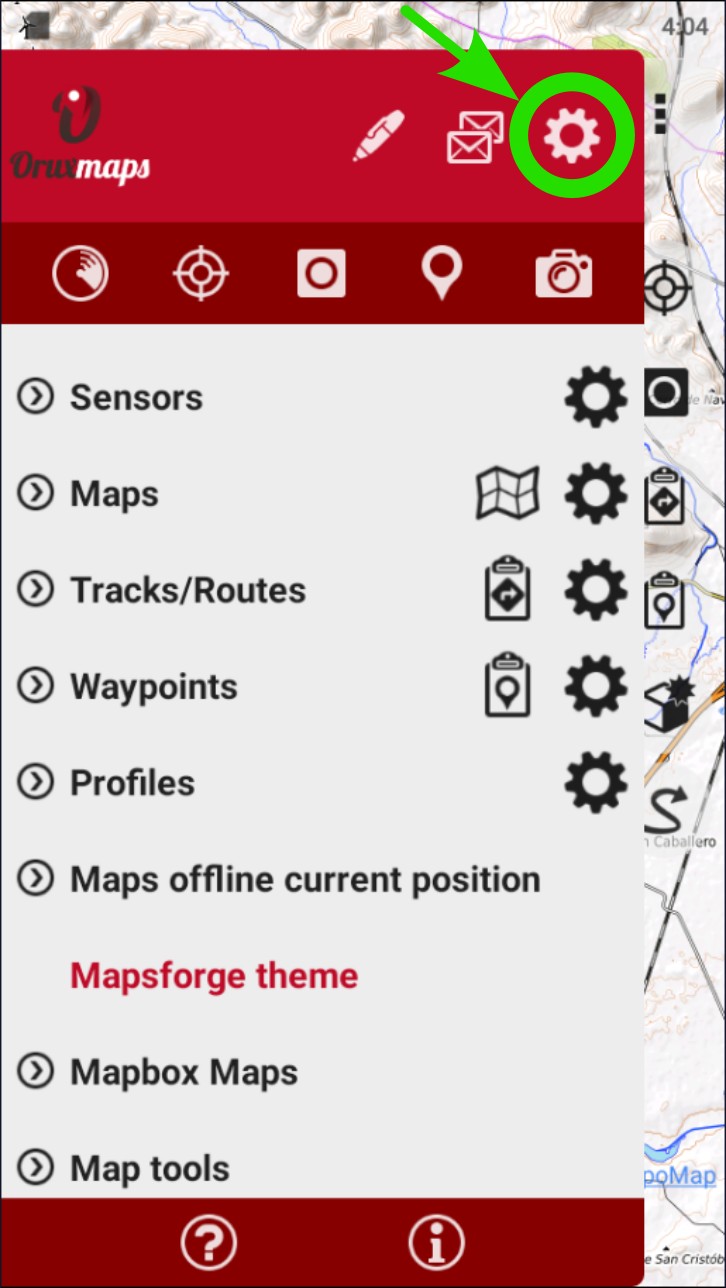
Buscar el menú "Integración" desplazando la pantalla hasta el final si no están visibles todas las opciones, esto dependerá de la resolución y configuración de la pantalla del smartphone
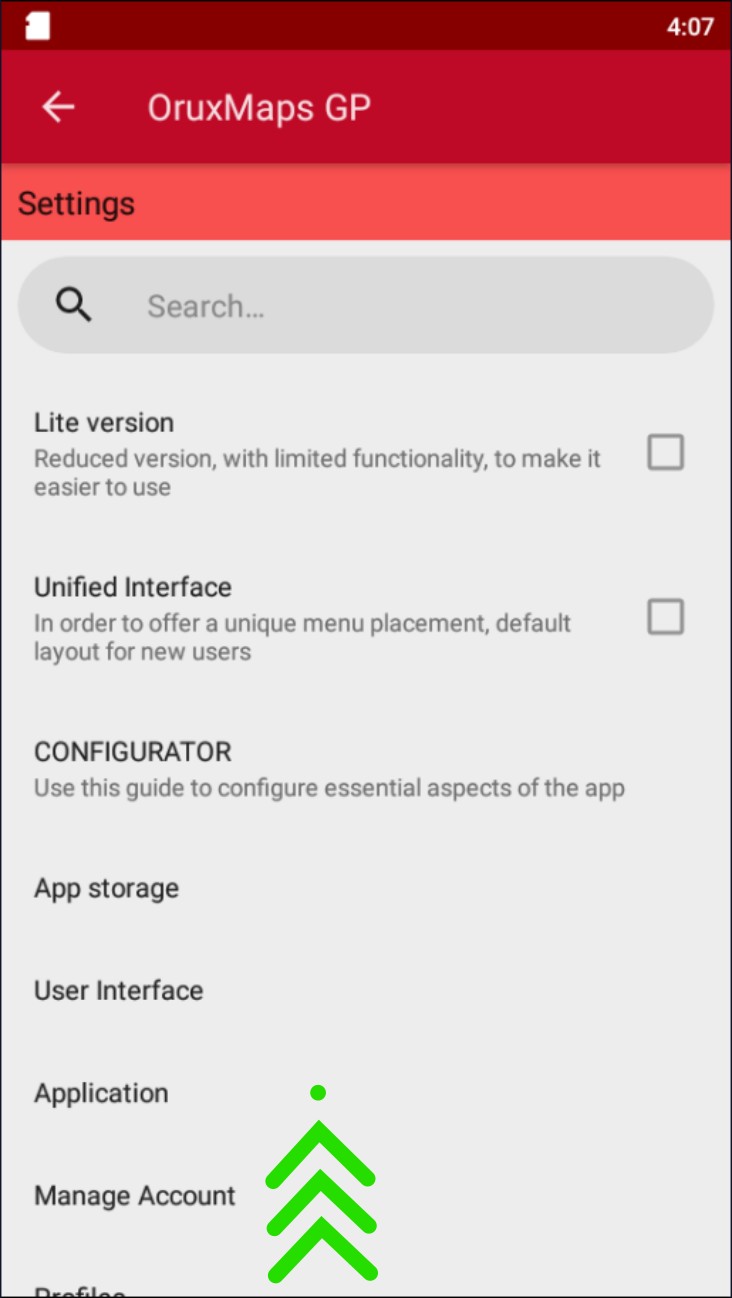
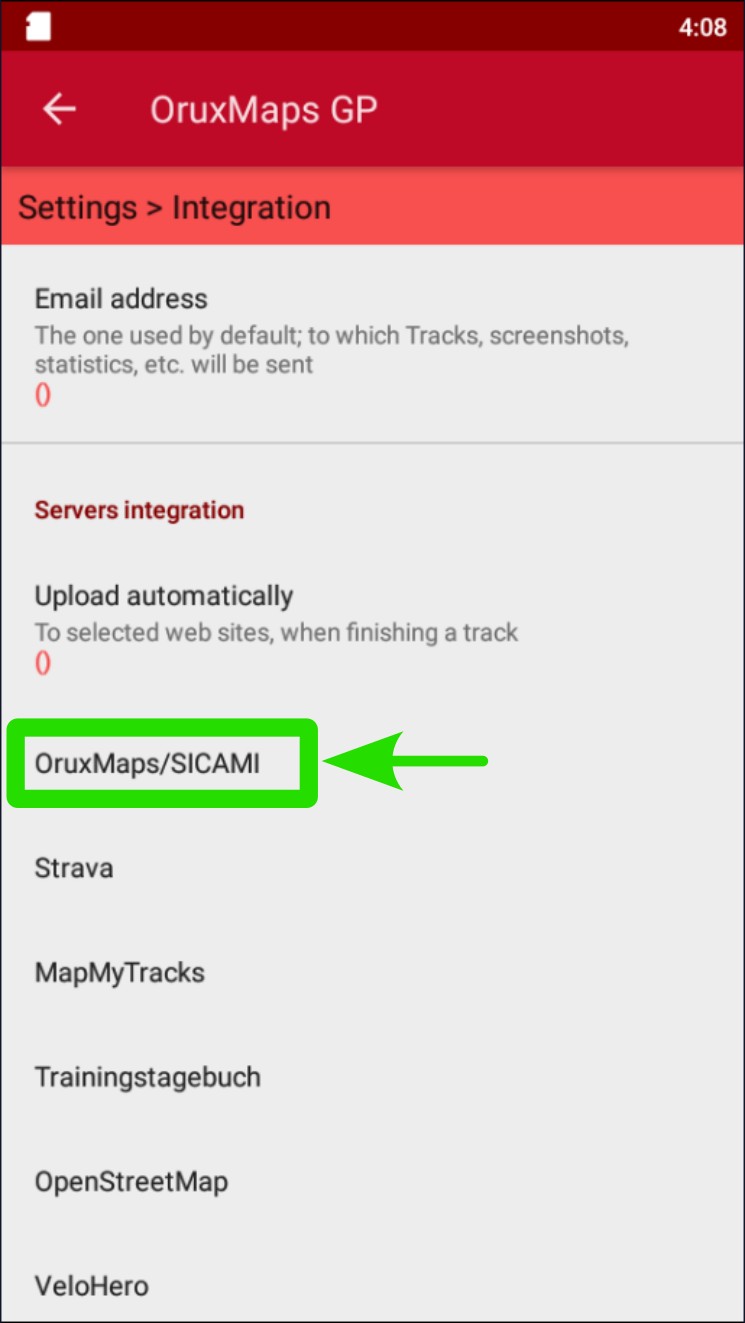
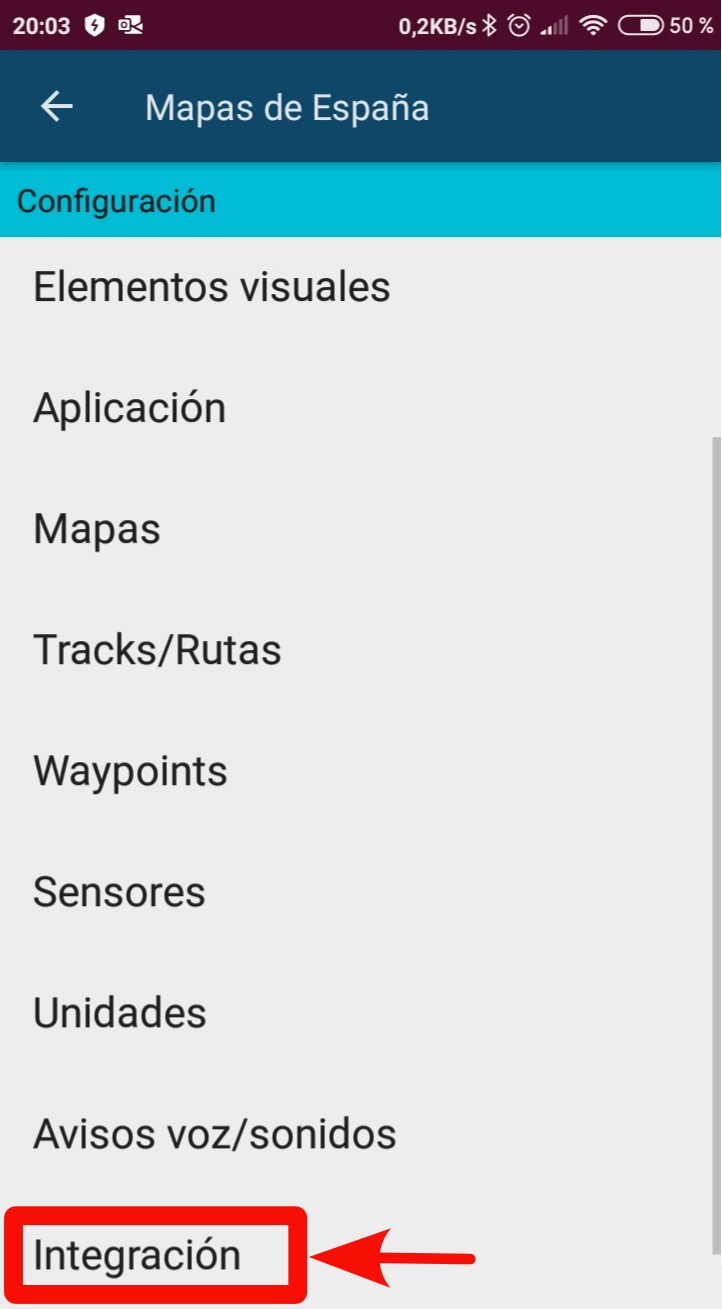
Pulsar sobre "Integración"
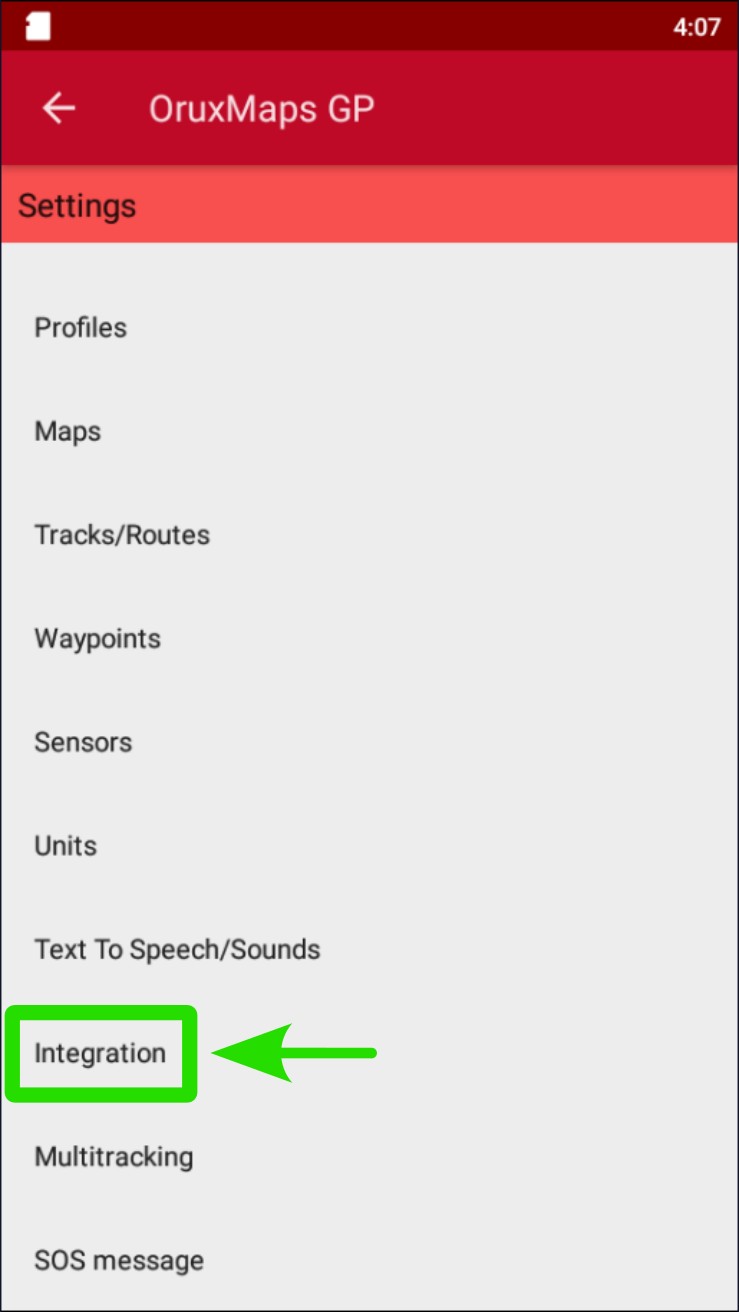
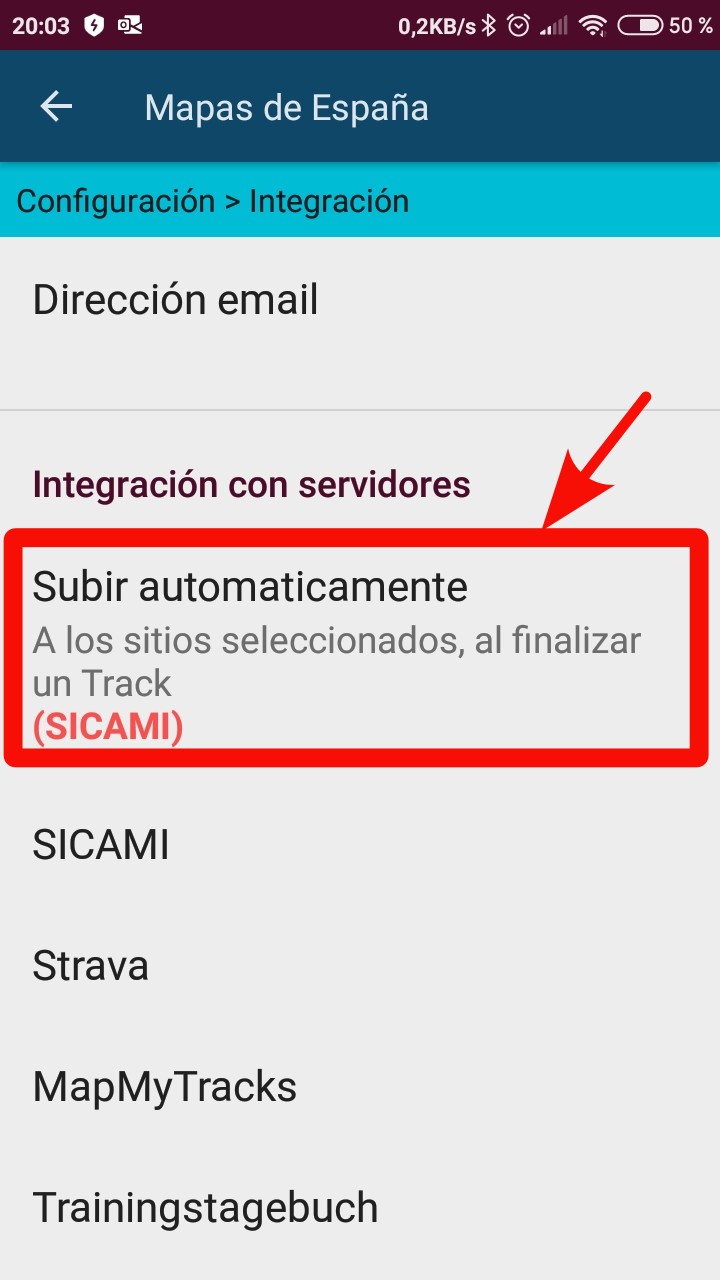
Pulsar sobre "Subir automáticamente"
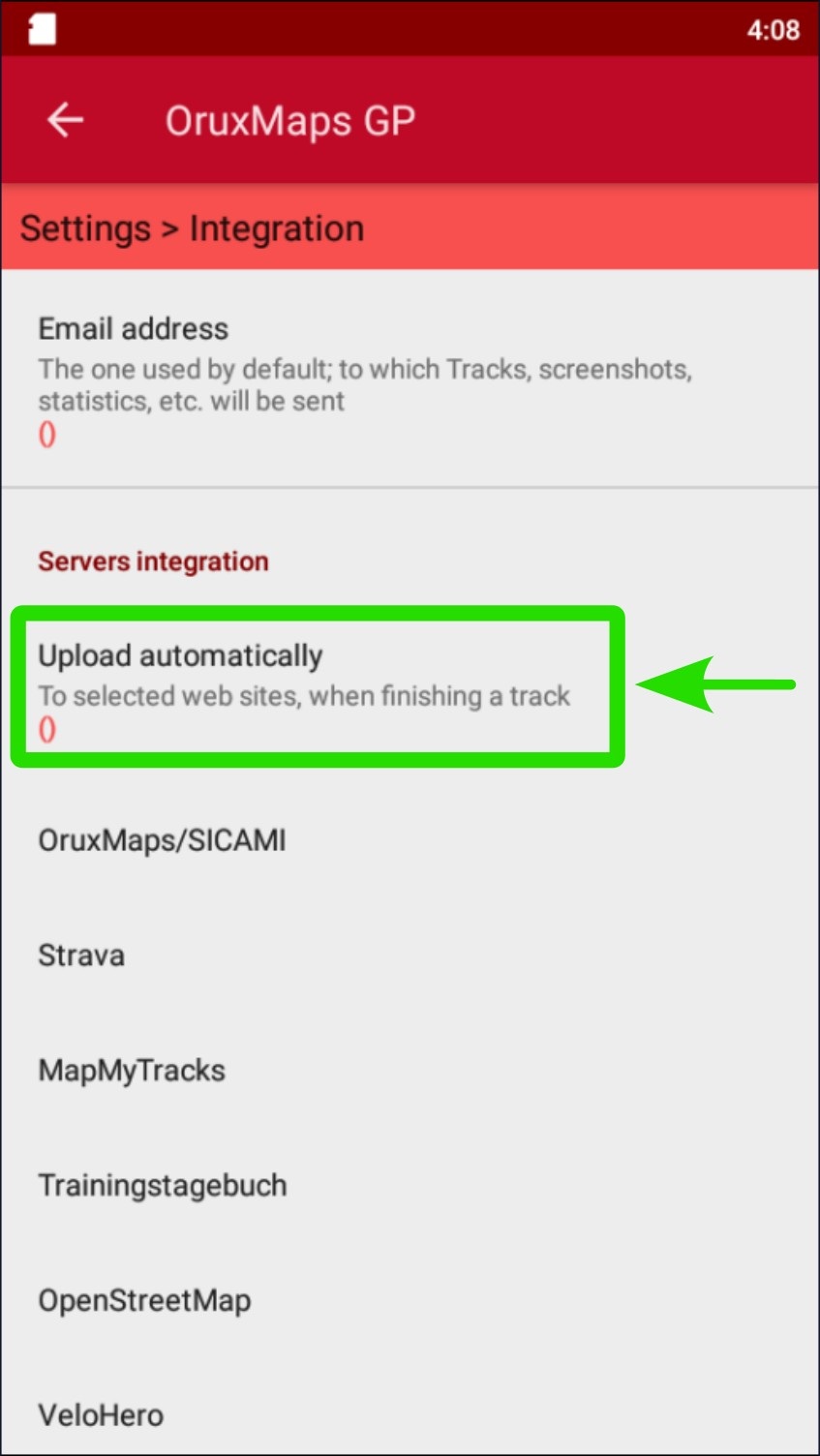
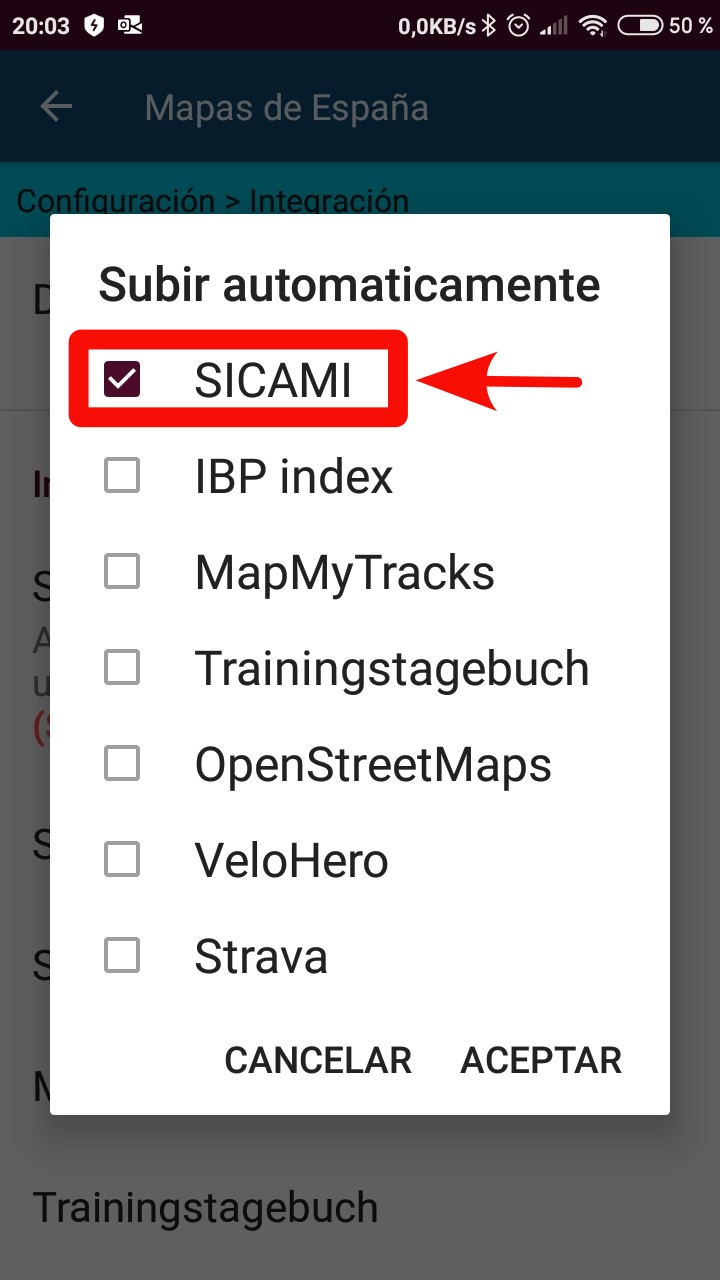
Marcar la casilla correspondiente a la aplicación que se desea vincular.
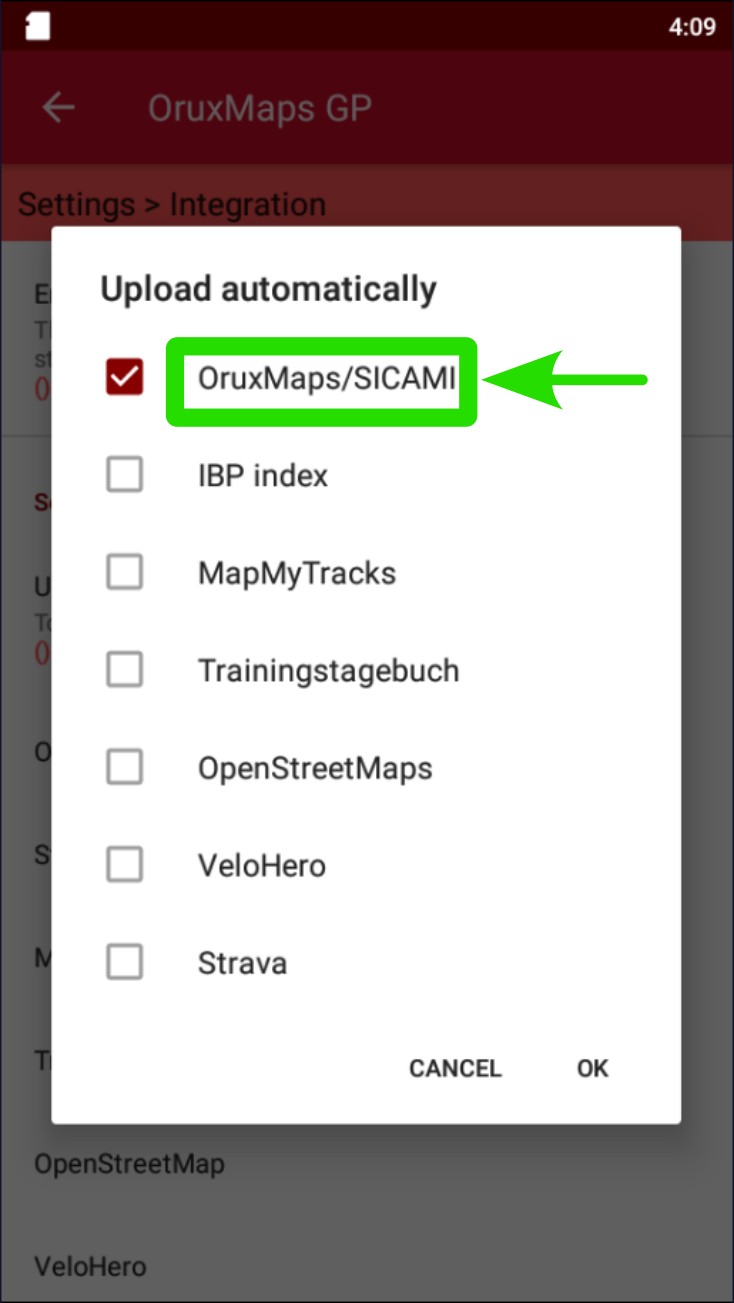
En caso de que no estuviera configurada la cuenta se solicitará la introducción de los datos correspondientes de la cuenta en SICAMI. Para el caso de Strava será necesario logearse en la pantalla emergente de Strava.
Configurar en esta pantalla la privacidad de las rutas que se suban automáticamente y si se desea que también se suban las fotografías de las rutas.
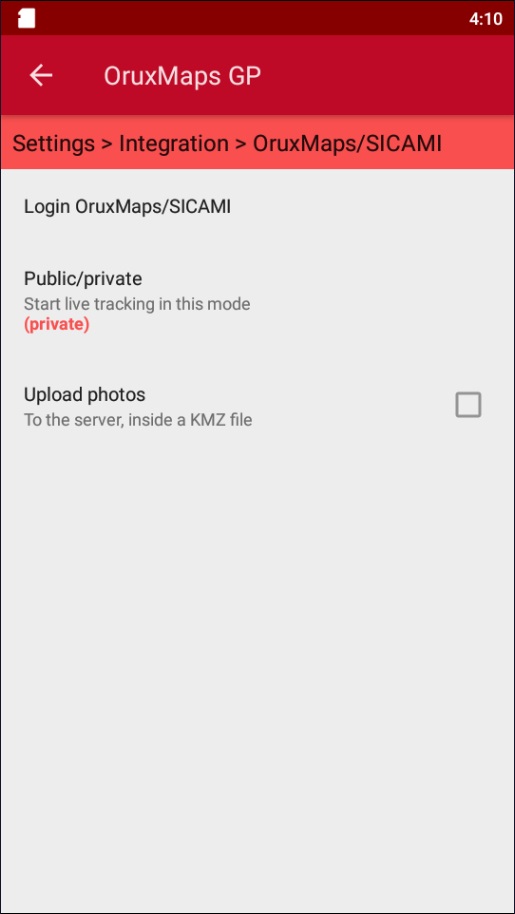
Estas opciones se pueden modificar posteriormente accediendo a "Integración" y seleccionando la aplicación vinculada.
Subir manualmente rutas a Sicami o Strava
Las rutas también se pueden transferir o subir manualmente a Sicami o Strava.
Para esto seguir los siguientes pasos:
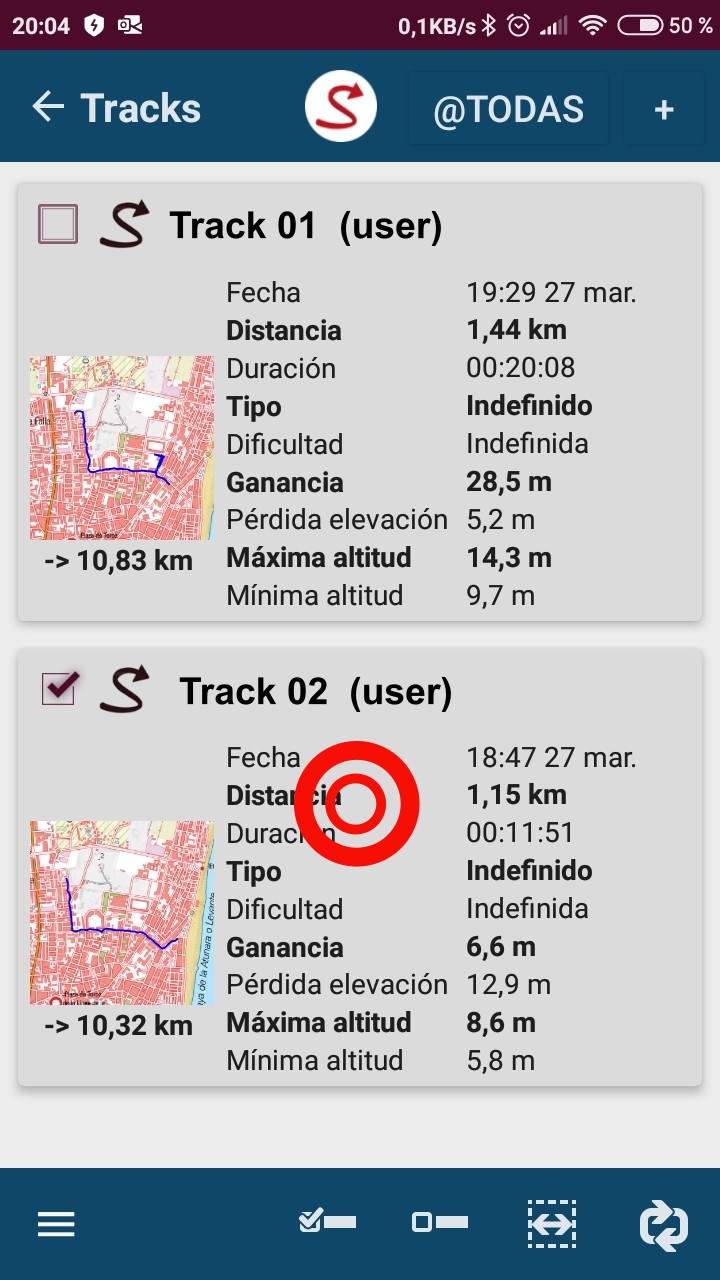
- Acceder a la lista de Tracks/Rutas.
- Hacer clic en la que se desee transferir.
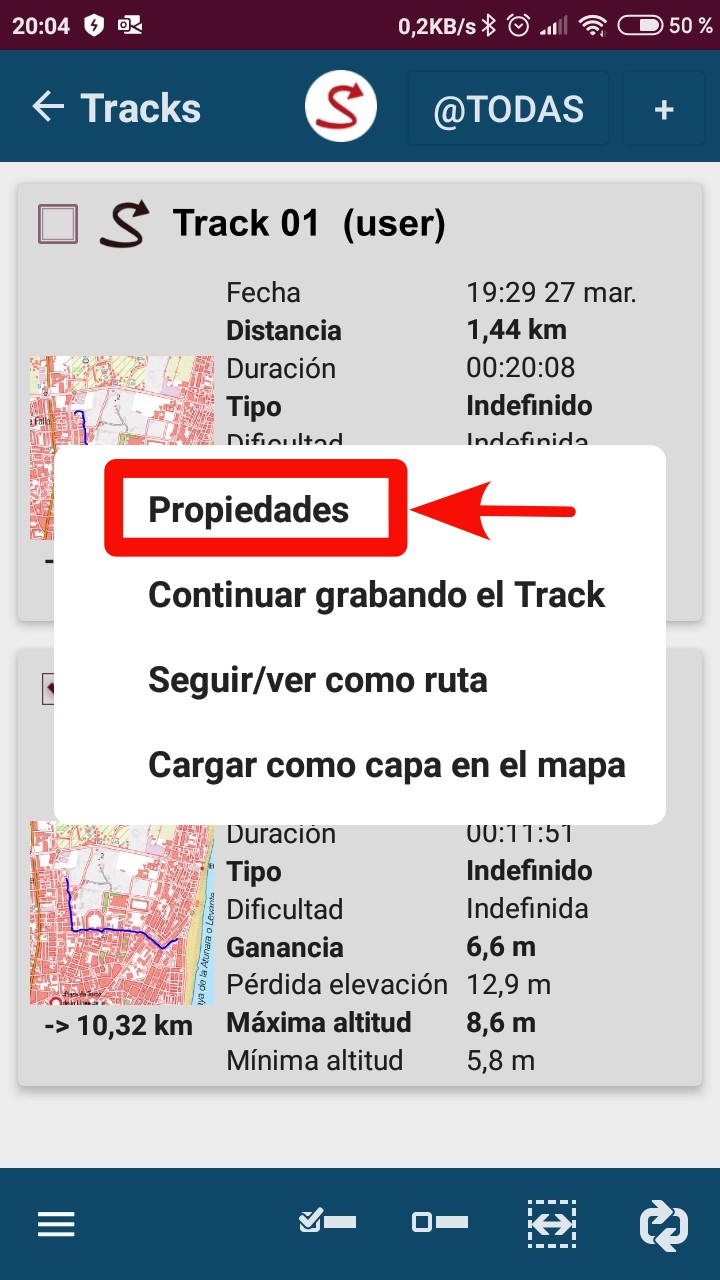
- Pulsar en "Propiedades" en la pantalla emergente.
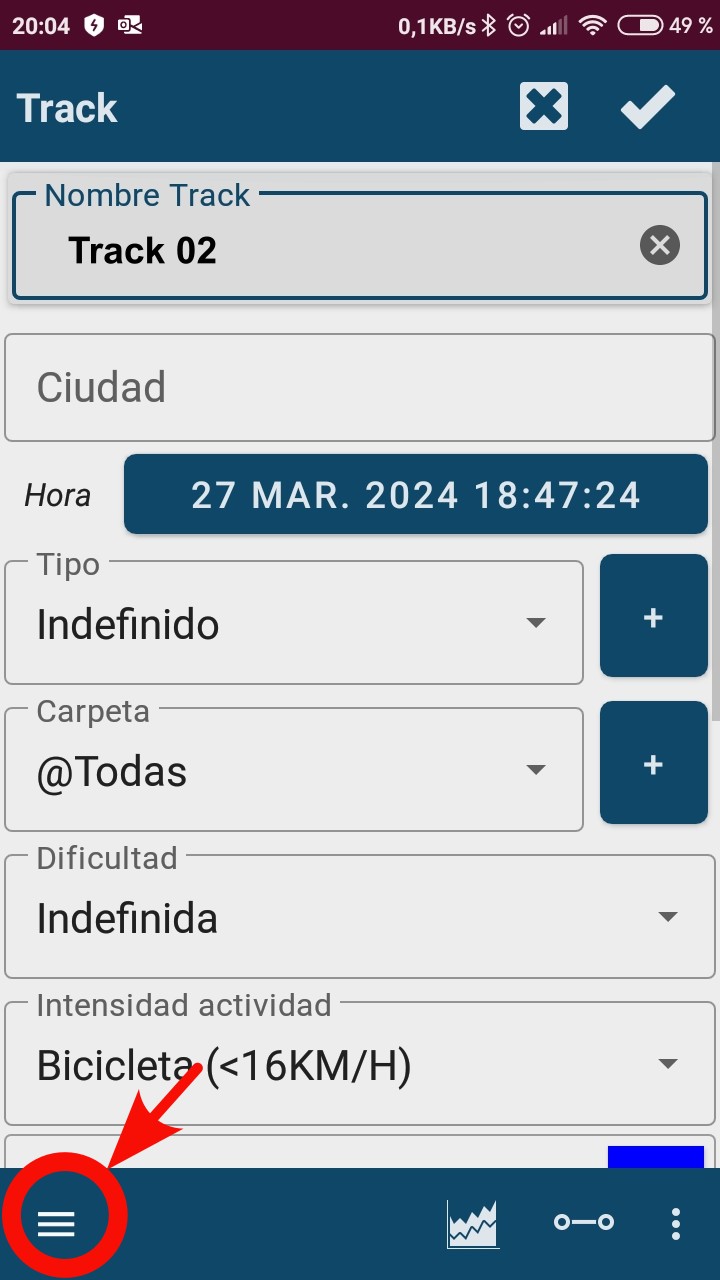
- Pulsar en el panel de configuración (tres líneas horizontales) en la esquina inferior izquierda.
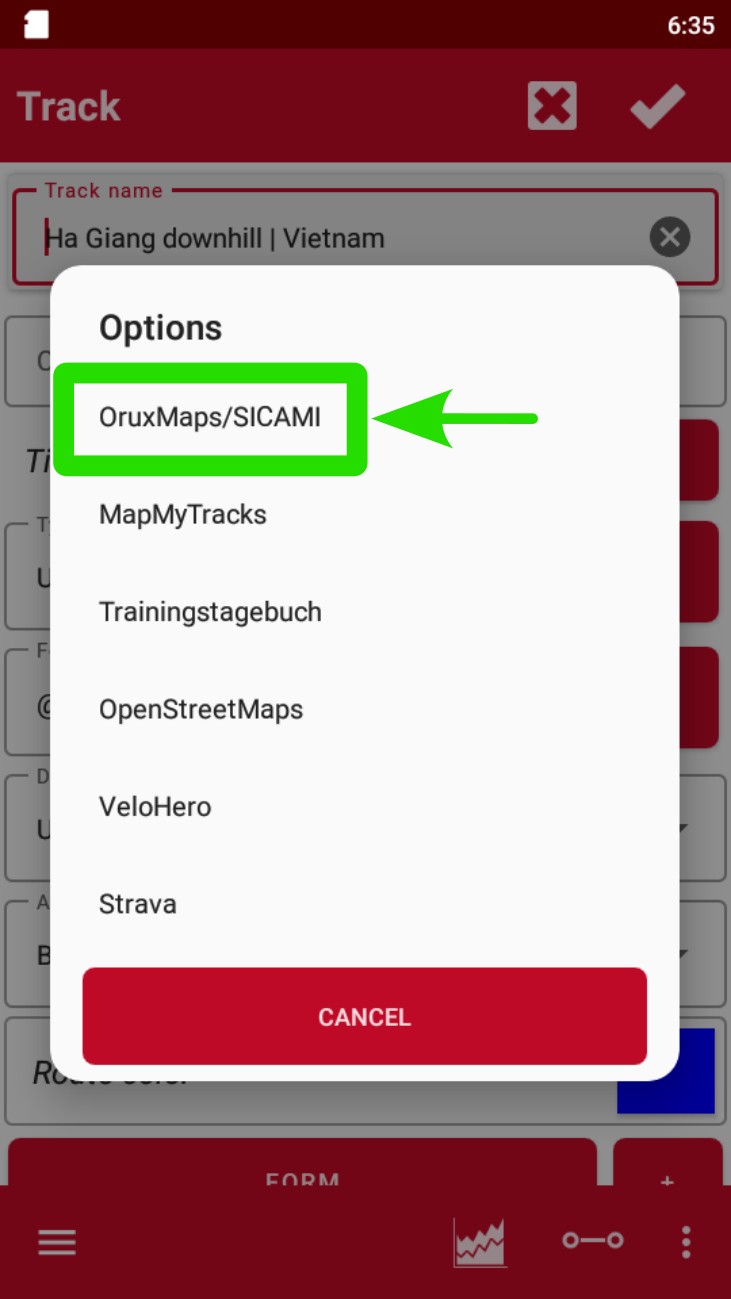
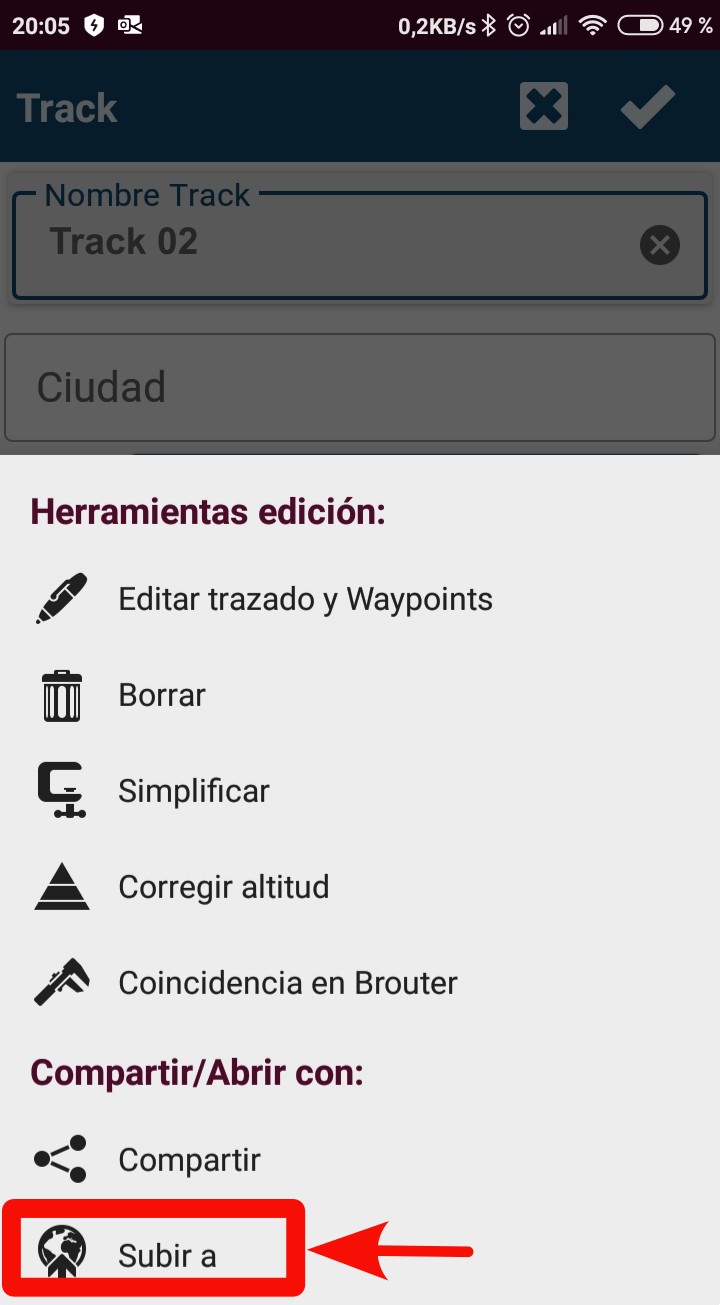
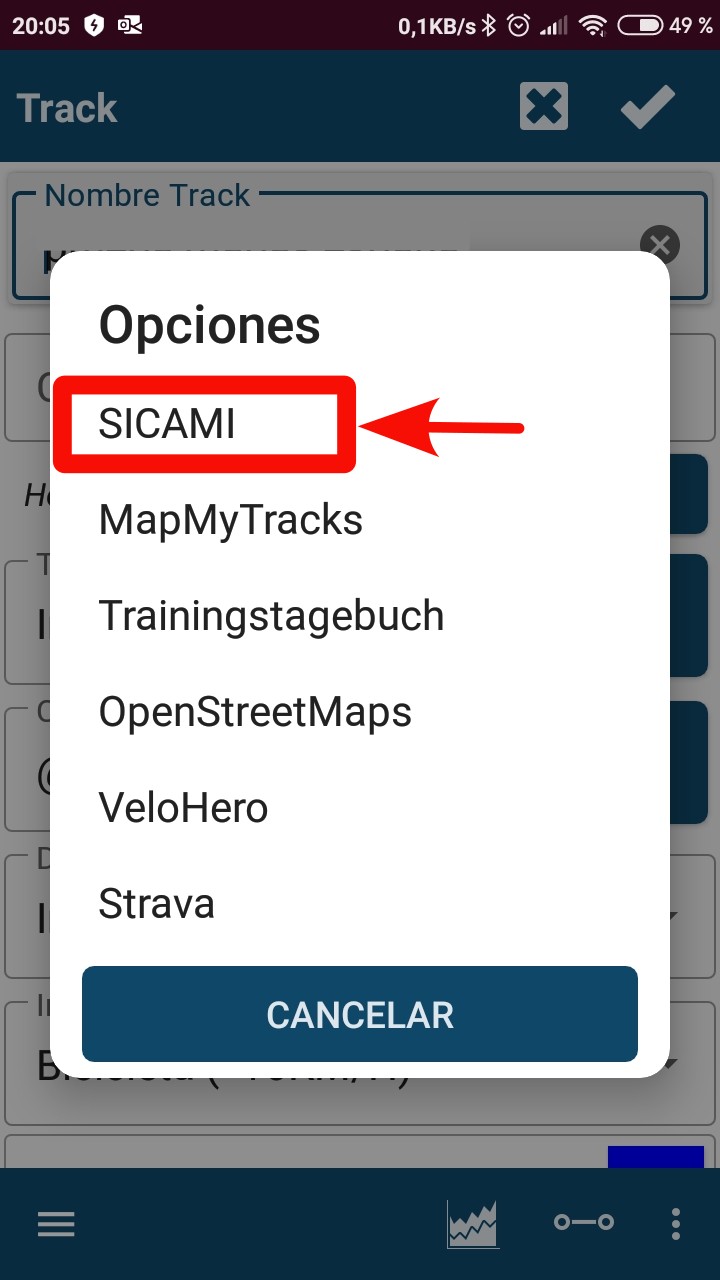
- Seleccionar "Subir a".
- Marcar "SICAMI" o Strava.
A continuación se muestran los pasos en imágenes sobre la pantalla.
Pulsar sobre el icono NAVEGACIÓN. También es accesible desde el botón "Tracks" en los botones laterales a la derecha
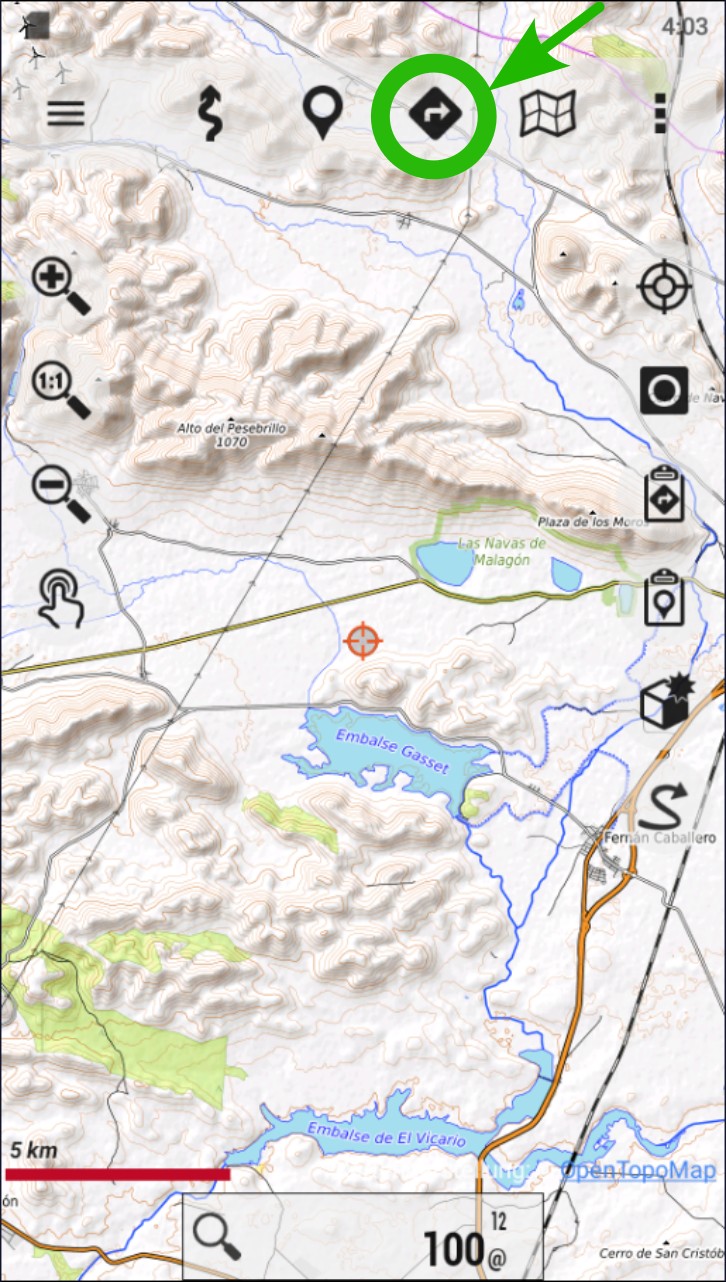
Ir a "Gestionar Tracks/Rutas".
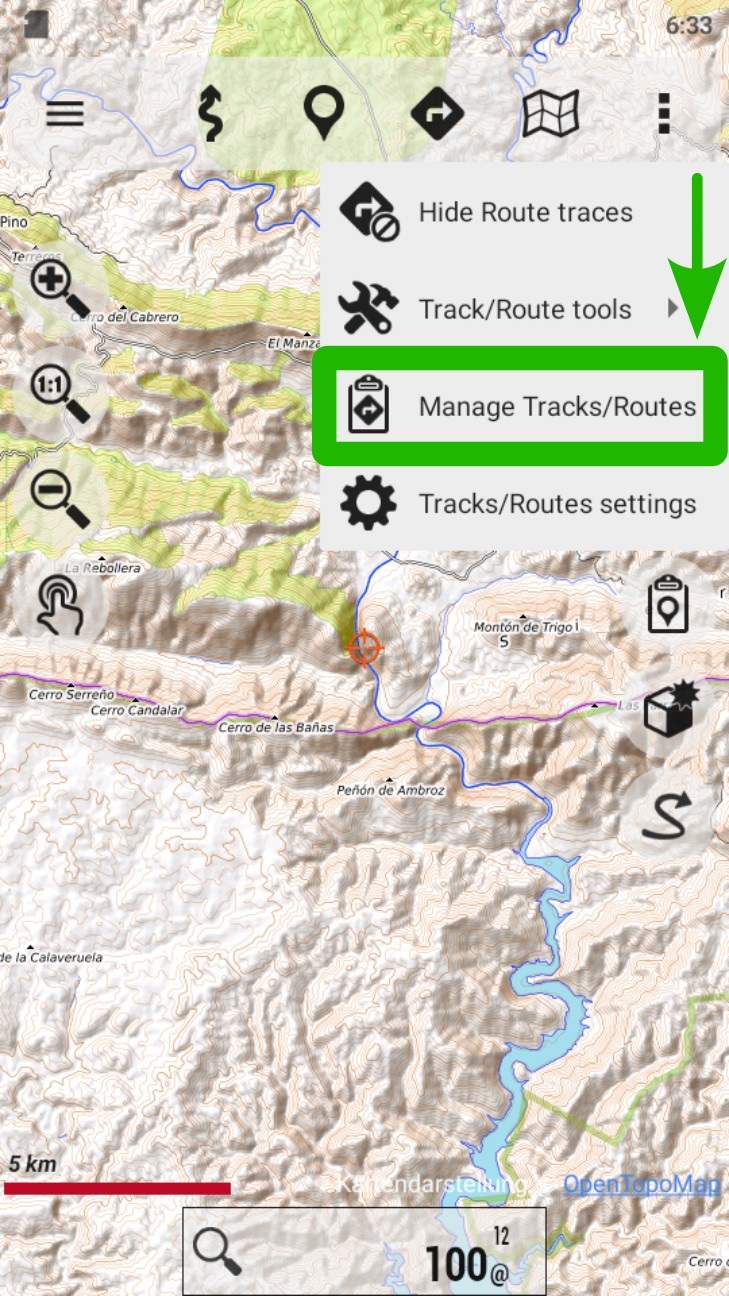
Toque sobre el Track/Ruta deseada para abrir el menú contextual.
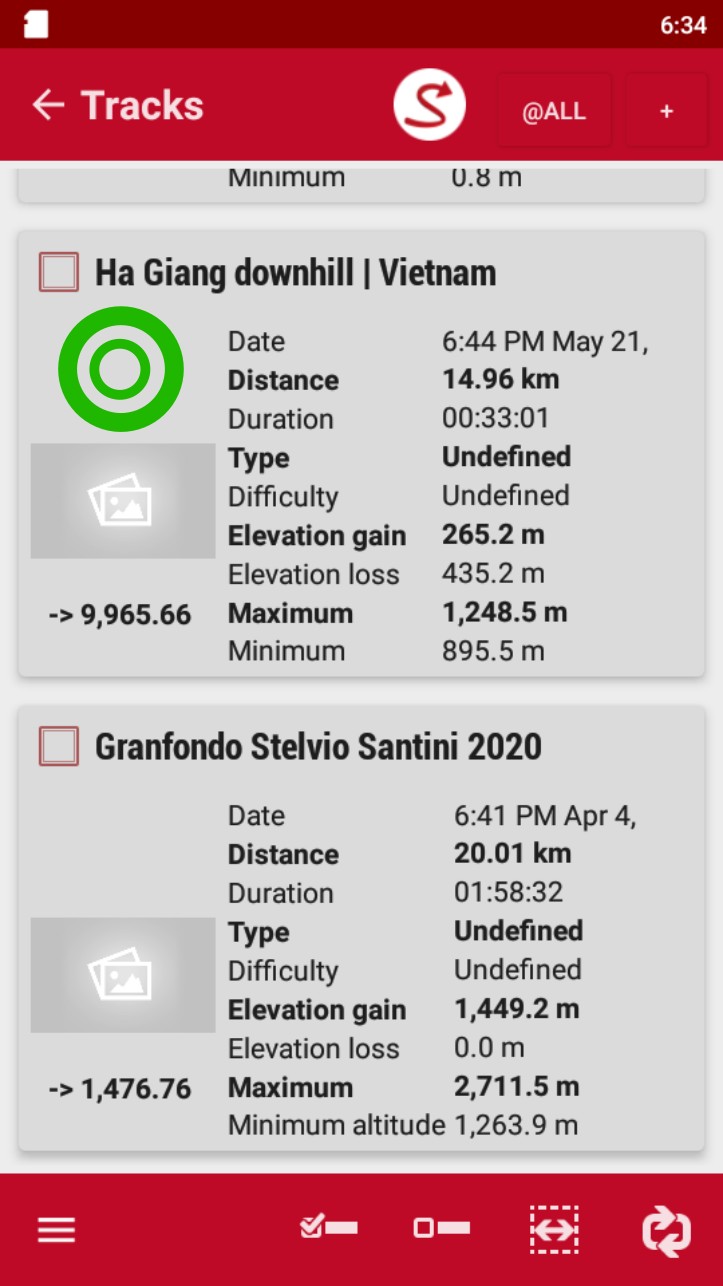
Ir a "Propiedades"
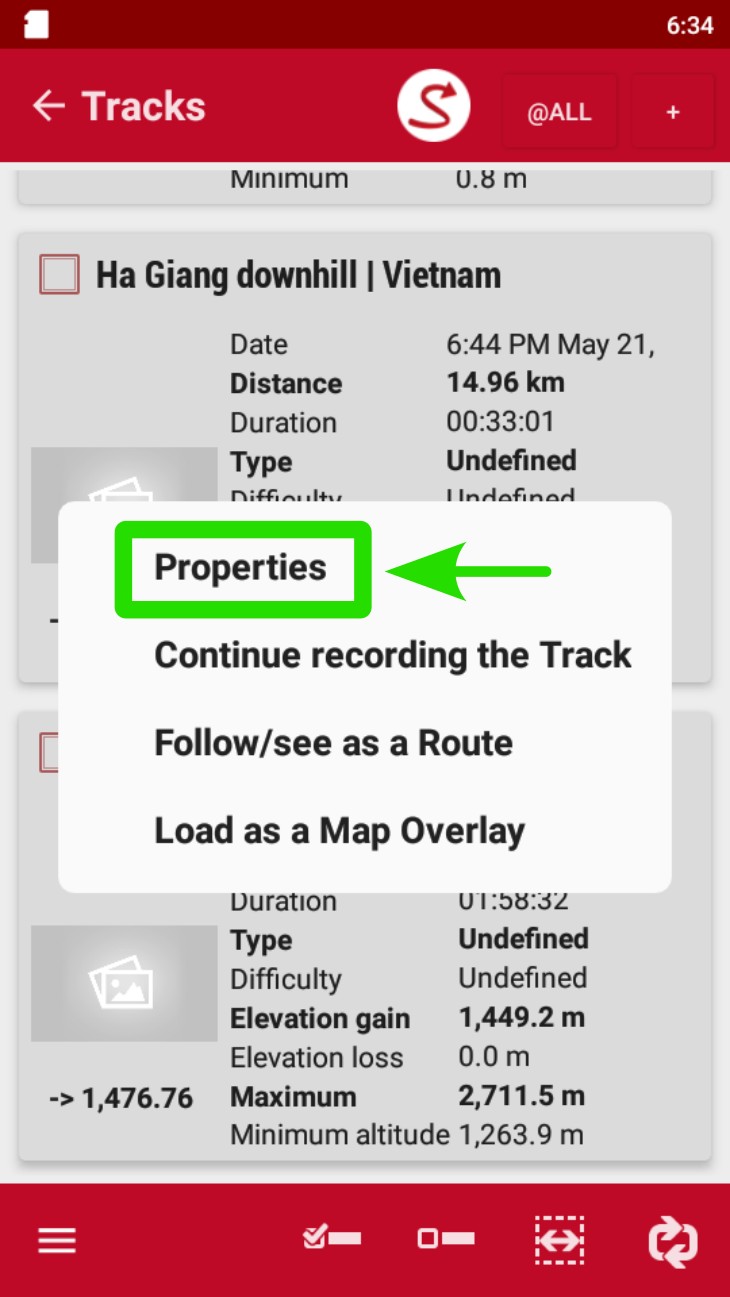
Pulsar sobre el panel de configuraciones inferior izquierdo
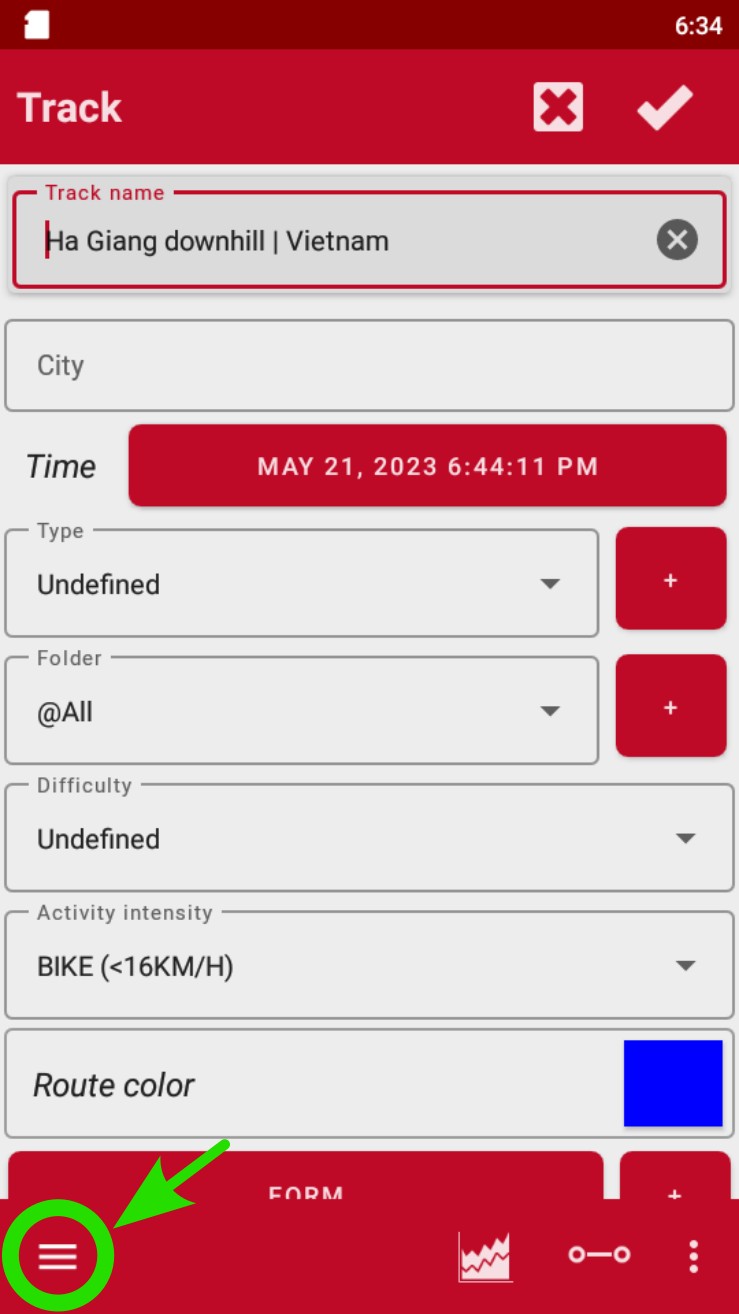
Pulsar sobre "Subir a"
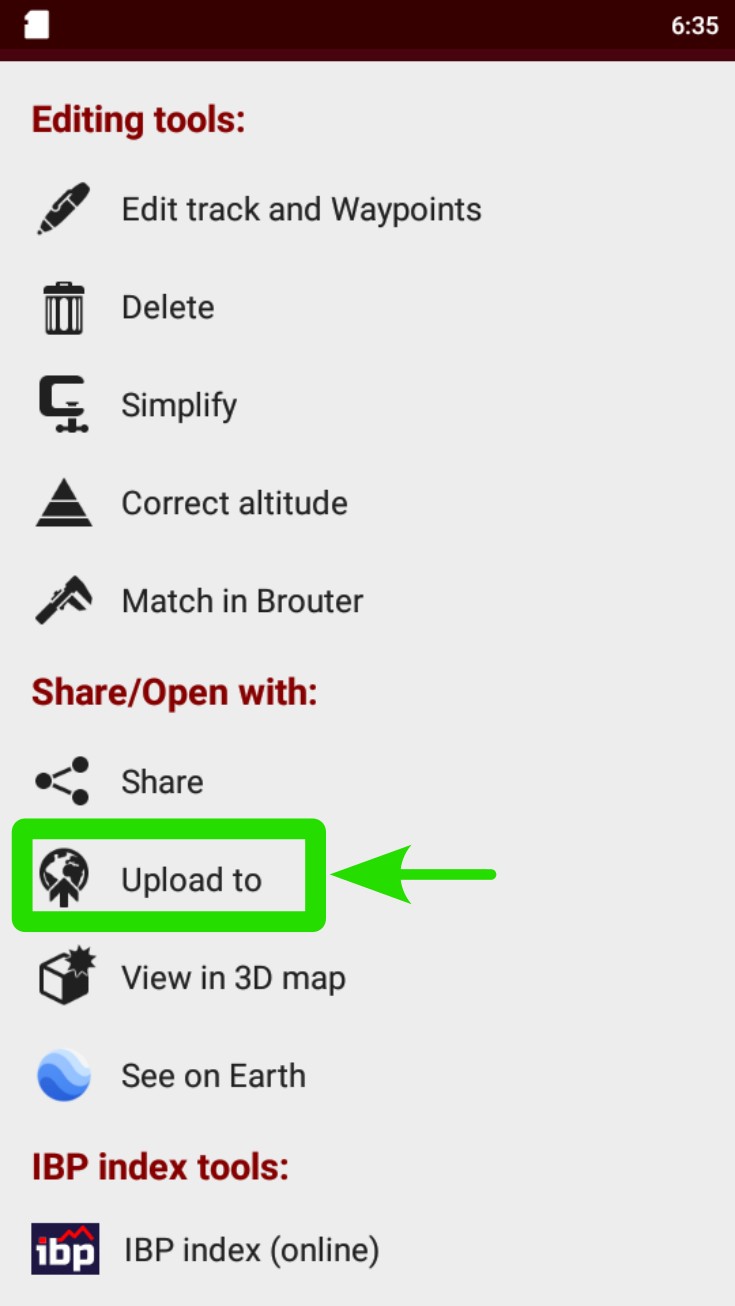
Seleccionar SICAMI, Strava o la aplicación deseada.
##publi##
Cómo conectar, vincular o integrar Mapas de España IGN con Sicami o Strava para transferir o exportar tracks y rutas automáticamente. Guía paso a paso con imágenes y vídeos.

Este procedimiento afectará a todas las nuevas rutas grabadas, pero no a las ya existentes que habrá que transferir manualmente. El procedimiento manual se indica al más adelante en este artículo
Esquema de la pantalla principal Mapas de España IGN con los elementos más destacados.

Ir a Configuración --> Integraciones --> Subir Automáticamente --> Marcar Sicami o Strava
Es imprescindible tener configuradas las cuentas correspondientes, si no lo estuvieran se solicitarán los datos o se indicará mediante un mensaje.
El procedimiento paso a paso sería el siguiente:
Pulsar sobre el icono del "Panel Lateral", (tres líneas horizontales en la zona superior izquierda). Esta opción también es accesible desde "Configurar la app" (icono con tres puntos en la zona superior derecha).
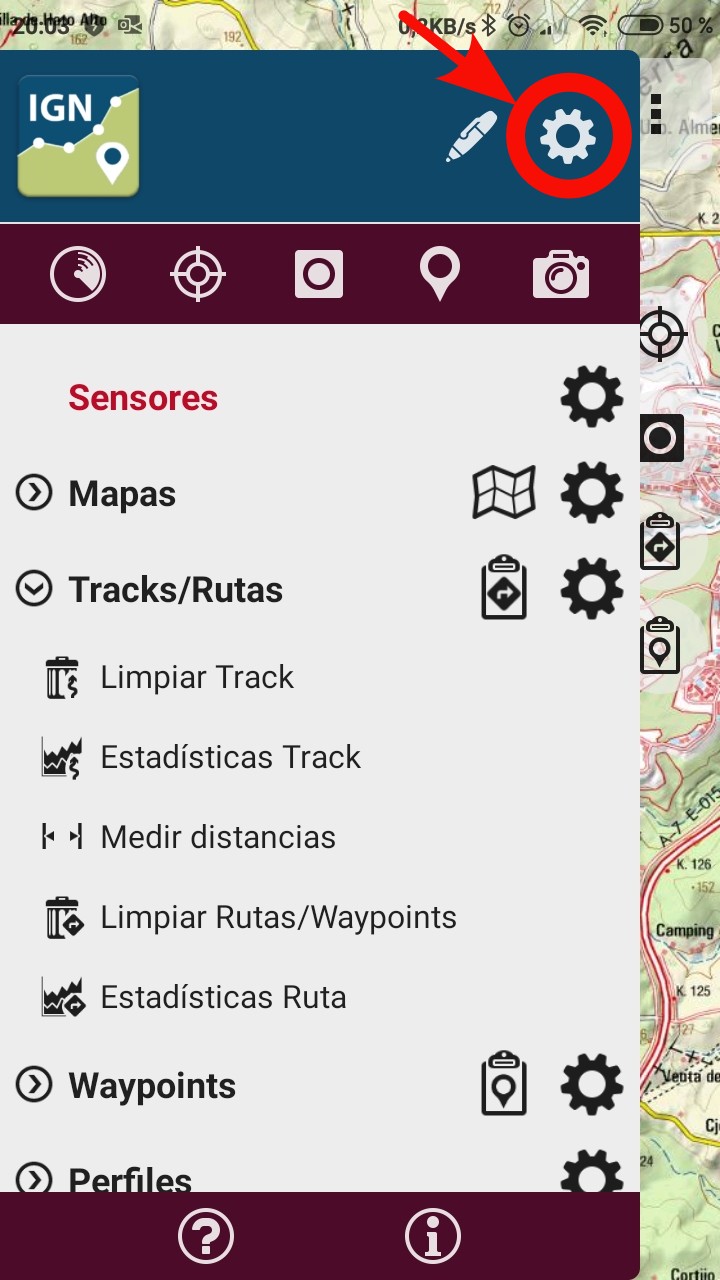
Acceder a "Configuración global" pulsando sobre el icono de rueda de configuraciones
Buscar el menú "Integración" desplazando la pantalla hasta el final si no están visibles todas las opciones, esto dependerá de la resolución y configuración de la pantalla del smartphone
Pulsar sobre "Integración"
Pulsar sobre "Subir automáticamente"
Marcar la casilla correspondiente a la aplicación que se desea vincular
En caso de que no estuviera configurada la cuenta se solicitará la introducción de los datos correspondinetes de la cuenta en SICAMI. Para el caso de Strava será necesario logearse en la pantalla emergente de Strava.
Configurar en esta pantalla la privacidad de las rutas que se suban automáticamente y si se desea que también se suban las fotografías de las rutas
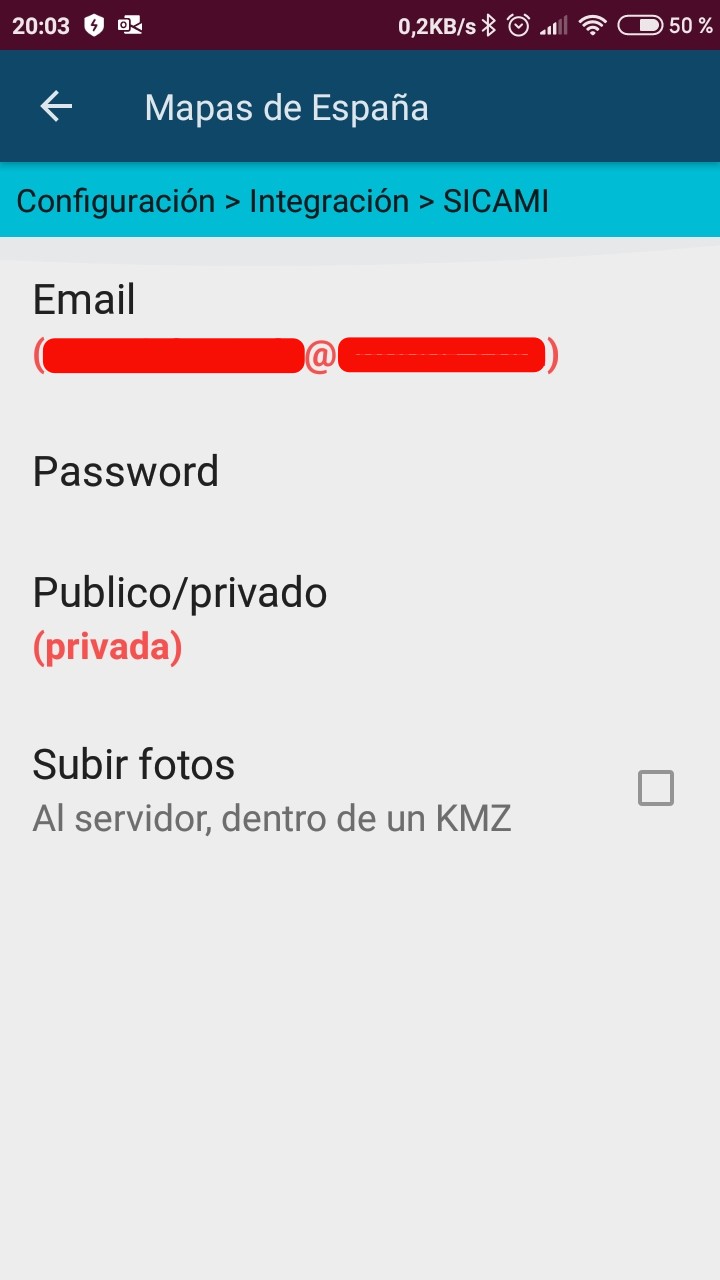
Estas opciones se pueden modificar posteriormente accediendo a "Integración" y seleccionando la aplicación vinculada.
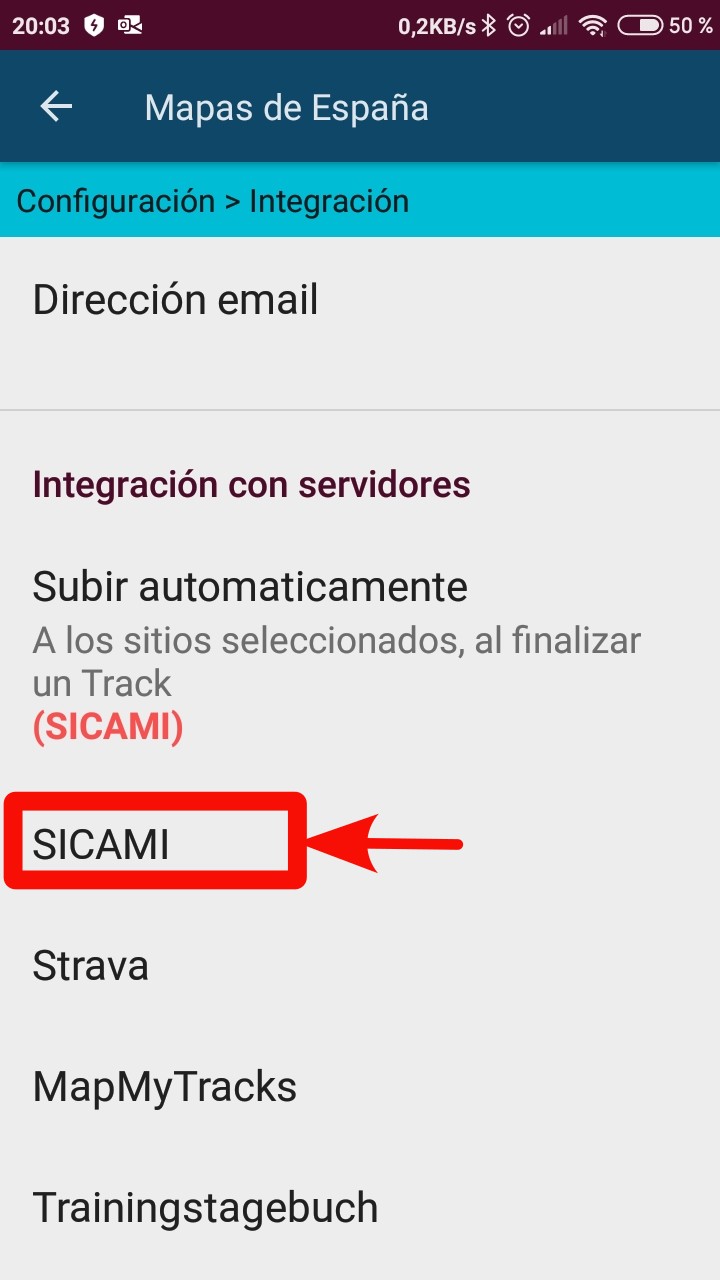
Subir manualmente rutas a Sicami o Strava
Las rutas también se pueden transferir o subir manualmente a Sicami o Strava.
Para esto seguir los siguientes pasos:
- acceder a la lista de Tracks/Rutas
- hacer clic en la que se desee transferir
- pulsar en "Propiedades" en la pantalla emergente
- pulsar en el panel de configuración (tres líneas horizontales) en la esquina inferior izquierda
- seleccionar "Subir a"
- Marcar "SICAMI" o Strava.
A continuación se muestran los pasos en un video y en imágenes sobre la pantalla
Pulsar sobre el icono NAVEGACIÓN. También es accesible desde el botón "Tracks" en los botones laterales a la derecha
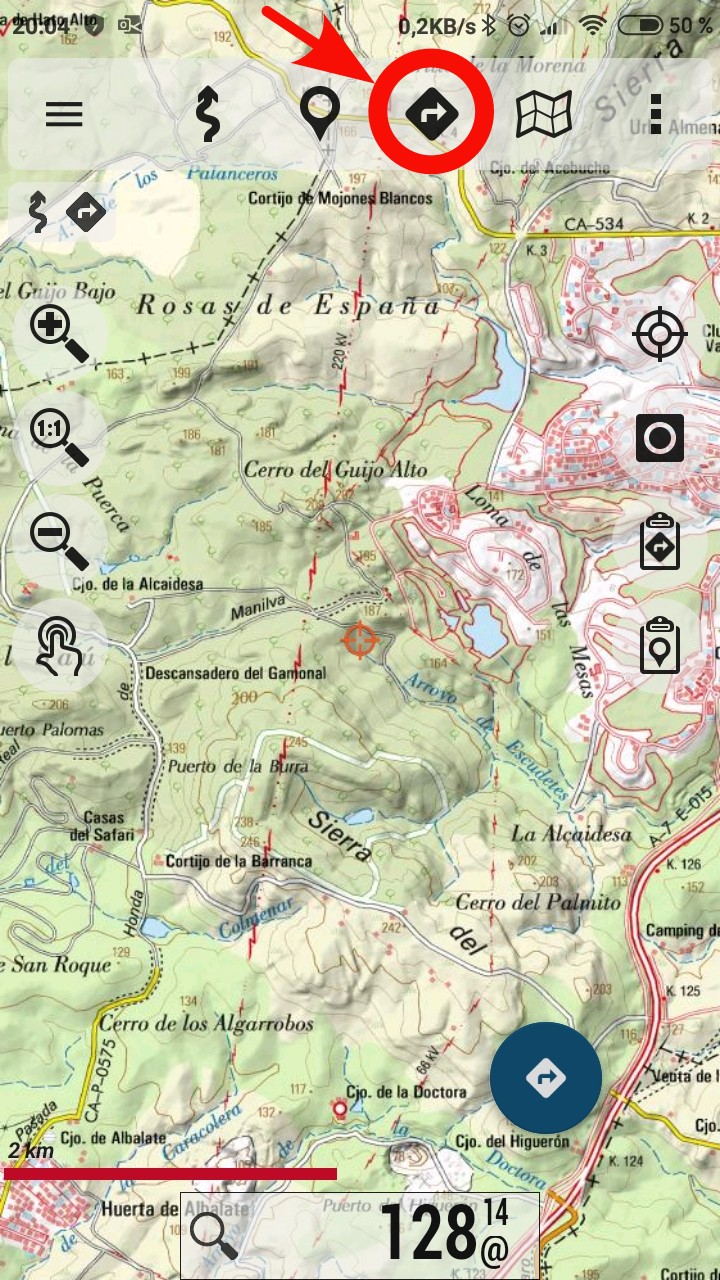
Ir a Gestionar Tracks/Rutas
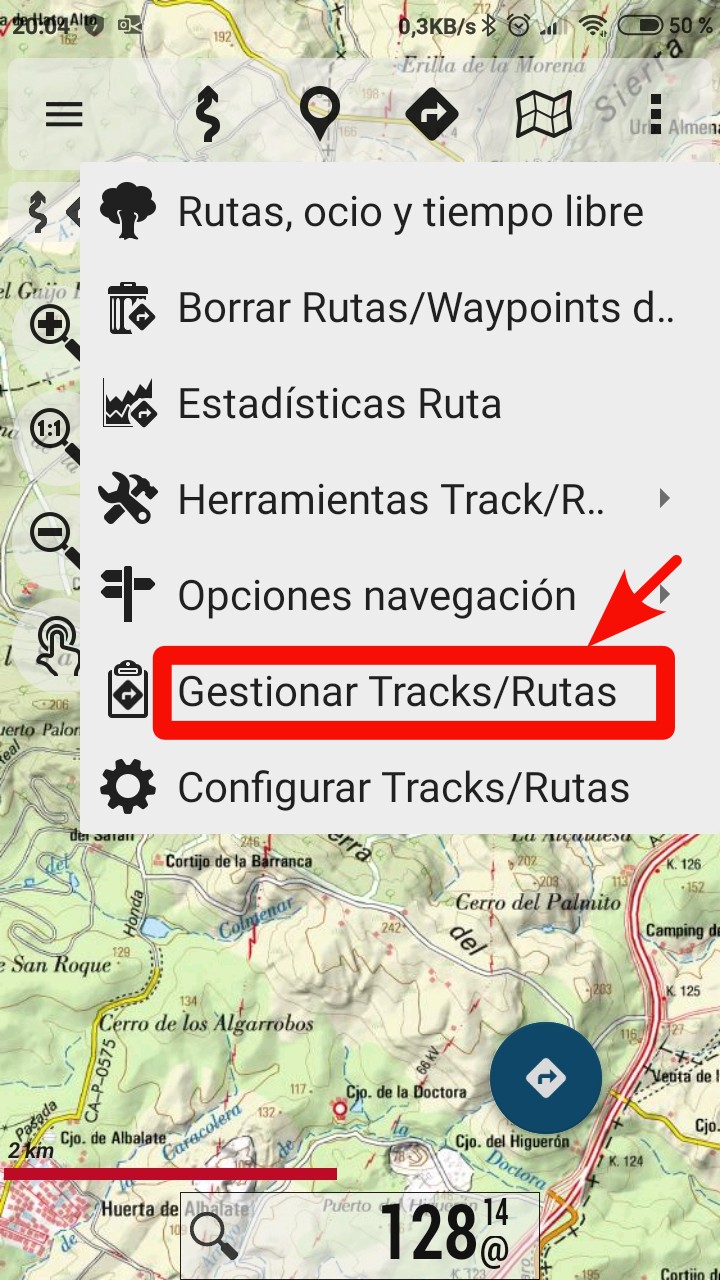
Toque sobre el Track/Ruta deseada para abrir el menú contextual
Ir a Propiedades
Pulsar sobre el panel de configuraciones inferior izquierdo
Pulsar sobre "Subir a"
Seleccionar SICAMI, Strava o la aplicación deseada
##publi##
Cómo transferir o exportar manualmente tracks y rutas desde Mapas de España IGN a Sicami o Strava. Guía paso a paso con imágenes y vídeos.

Esquema de la pantalla principal Mapas de España IGN con los elementos más destacados.

Las rutas también se pueden transferir o subir manualmente a Sicami o Strava, para esto seguir los siguiente pasos.
- acceder a la lista de Tracks/Rutas
- hacer clic en la que se desee transferir
- pulsar en "Propiedades" en la pantalla emergente
- pulsar en el panel de configuración (tres líneas horizontales) en la esquina inferior izquierda
- seleccionar "Subir a"
- Marcar "SICAMI" o Strava.
A continuación se muestran los pasos en un video y en imágenes sobre la pantalla
Pulsar sobre el icono NAVEGACIÓN. También es accesible desde el botón "Tracks" en los botones laterales a la derecha

Ir a Gestionar Tracks/Rutas

Toque sobre el Track/Ruta deseada para abrir el menú contextual

Ir a Propiedades

Pulsar sobre el panel de configuraciones inferior izquierdo

Pulsar sobre "Subir a"

Seleccionar SICAMI, Strava o la aplicación deseada

##publi##
Aerodinámica fácil para ciclistas y algunos consejos
Aerodinámica fácil en el ciclismo y algunos consejos
La aerodinámica es la rama de la dinámica de fluidos que trata de describir y cuantificar las fuerzas que actúan sobre un objeto sumergido en un fluido gaseoso, que suele ser el aire, cuando el objeto se mueve, cuando el fluido se mueve o cuando ambos se mueven.
Cualquier ciclista que alguna vez haya pedaleado con viento en contra ha experimentado lo agotador que resulta atravesar la invisible masa de aire en movimiento que tiene delante. También habrá notado que cuanto más rápido va, más resistencia del aire experimenta y más energía debe ejercer para superarla. A esta fuerza o resistencia que se opone al avance la llamamos resistencia aerodinámica.
La presión y el rozamiento del aire
Podemos dividir la resistencia aerodinámica en dos componentes a vencer:
• la resistencia debida a la presión del aire
• la fricción directa o rozamiento del aire contra las superficies del ciclista y la bicicleta.
La presión del aire. Diferencia de presiones
El ciclista en movimiento perturba el aire que fluye a su alrededor, obligando al aire a separarse de su superficie para dejarle paso. Esto aumenta la presión en la parte delantera. Por otro lado, en la parte posterior del ciclista se produce el efecto contrario, creándose regiones de menor presión que dan como resultado un “arrastre de presión” contra el ciclista.
Al existir alta presión delante y baja presión detrás, el ciclista es literalmente arrastrado hacia atrás.
Los diseños aerodinámicos y la ropa ajustada ayudan a que el aire circule más suavemente alrededor de estos cuerpos y reducen la resistencia a la presión, minimizando además las turbulencias que se producen al atravesar el aire utilizando formas en los perfiles especialmente diseñadas a tal efecto.
El rozamiento del aire
La fuerza de fricción tiene menor magnitud y es producto del rozamiento del aire que está en contacto con la superficie exterior del ciclista y de la bicicleta.
En recorridos llanos, la resistencia aerodinámica es, con diferencia, la mayor barrera para el avance de un ciclista, pudiendo representar entre el 70 y el 90 por ciento de la resistencia que se siente al pedalear.
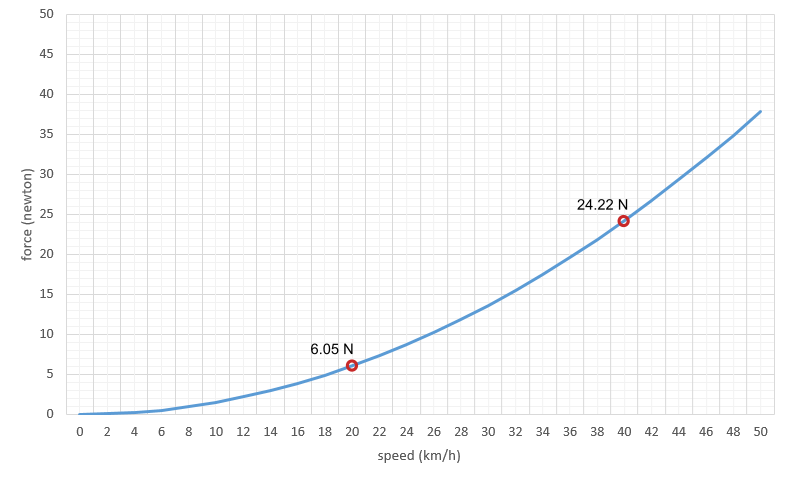
Fórmula matemática de la resistencia aerodinámica
Para entender mejor cómo afectan cada uno de los elementos en juego, vamos a estudiar, sin entrar en demasiadas profundidades, la conocida fórmula de la fuerza de rozamiento o de resistencia aerodinámica de un cuerpo con el aire.
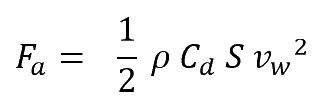
En esta fórmula:
- ρ es la densidad del aire en kg/m3. Es variable en función de la altitud y de otros parámetros como la temperatura (inversamente proporcional) o la presión atmosférica (directamente proporcional).
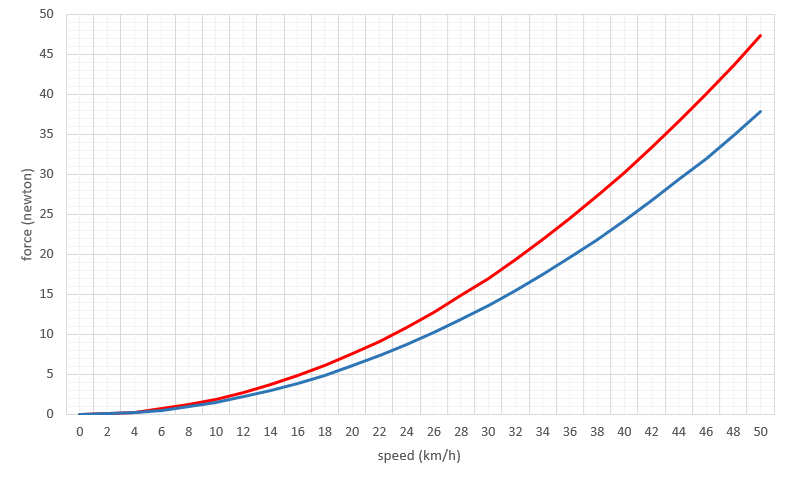
- Vw es la velocidad relativa, en metros por segundo, entre el aire y el ciclista, para vientos en contra se sumará la velocidad del ciclista a la velocidad del viento.
- Cd es el coeficiente de arrastre, que es una propiedad de la forma y la textura superficial del objeto. Es adimensional (no tiene unidades).
- S es el área transversal o proyectada frontal, en m2, del conjunto ciclista bicicleta. No se trata de la superficie total, si no del área que ocupa el conjunto ciclista-bicicleta visto frontalmente.


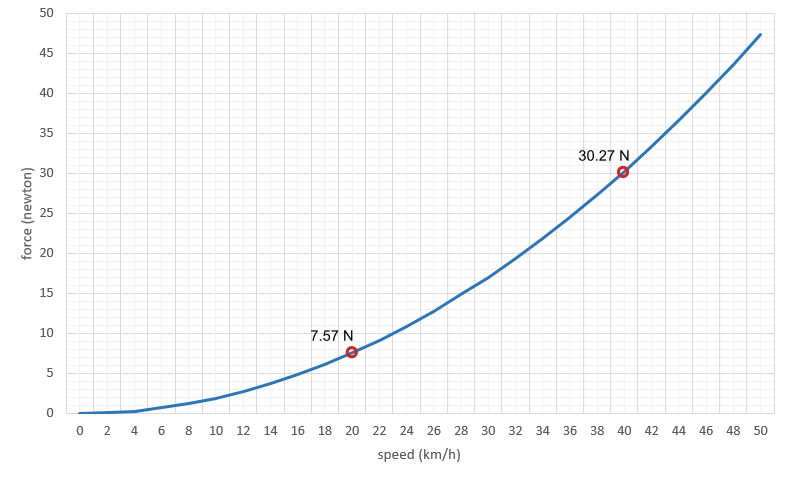
Conclusiones y recomendaciones
Para cicloturistas, ciclistas recreativos o aquellos a los que nos les preocupen sus marcas, parece que la mejor estrategia para afrontar vientos en contra sería reducir la velocidad, exactamente la misma que para enfrentar un ascenso y tomárselo con calma. Además de adoptar una postura y equipamiento que reduzca el área frontal expuesta en la medida de lo posible.
En escenarios más competitivos deberíamos plantearnos:
- Intentar ser más eficientes aerodinámicamente en los momentos de mayor velocidad, tales como tramos llanos y descensos.
- Relajar la posición en tramos de baja velocidad, tales como ascensos, donde la resistencia aerodinámica va perdiendo importancia a favor de la fuerza de la gravedad que vendrá determinada por el peso del conjunto ciclista-bicicleta.
Tan importante como lo anterior es que la posición sobre la bicicleta permita continuar pedaleando de forma cómoda, de modo que el esfuerzo y la fatiga sean sostenibles en el tiempo. La posición más rápida será aquella en la que minimicemos el impacto de la resistencia aerodinámica, pero que podamos mantener durante el mayor tiempo posible.
Artículos recomendados: Física del ciclismo: Fuerzas. Nociones básicas.
Rutas de senderismo
Rutas de senderismo. Conceptos y definiciones.
Un sendero es un camino estrecho, normalmente localizado en zonas rurales o regiones naturales, habilitado principalmente para el tránsito de peatones y ganado. Cuando este tránsito es más elevado, tienden a hacerse más amplios y se convierten en veredas. Permiten el paso a través de estas regiones y en ocasiones conectan pueblos pequeños y aldeas entre sí o con puntos de interés ganadero, agrícola o paisajístico.

Lo habitual es que estos caminos no estén señalizados ni dispongan de ningún tipo de pavimento o acondicionamiento para la circulación de vehículos, siendo recorridos principalmente a pie, en bicicleta, motocicleta o a caballo.

Una ruta de senderismo es aquella ruta, a realizar a pie, que discurre principalmente por este tipo de vías, pudiendo estar compuesta por senderos, veredas, cañadas, cañadas reales, caminos reales, cortafuegos…, siendo el senderismo la práctica de ocio consistente en caminar transitando por caminos de estas características. En la actualidad, se trata de una actividad en auge que permite disfrutar de la naturaleza y que puede ser realizada por personas de todas las edades y niveles, existiendo gran variedad de recorridos, con diferente dificultad y duración.
Seguir una ruta de senderismo
Para seguir una ruta de senderismo y no perderse en el camino, es conveniente disponer de un mapa, preferiblemente topográfico, que represente los distintos accidentes geográficos y sobre el que tengamos marcado el recorrido. Además de instrumentos para calcular la posición y la orientación, como una brújula.

Actualmente, existen mapas topográficos digitales que pueden ser utilizados en dispositivos GPS dedicados o teléfonos móviles que, junto a los sistemas de posicionamiento por satélite GPS, permiten obtener y visualizar la posición en el mapa con gran exactitud.
También existen aplicaciones específicas que permiten cargar la ruta de senderismo y mostrarla sobre el mapa de modo que seguirla sea fácil, muy visual e intuitivo.
Crear una ruta de senderismo
Existen diferentes formas de crear una ruta de senderismo, aunque lo más habitual es generarlas automáticamente conforme se realizan sobre el terreno o dibujándolas sobre un mapa en una aplicación que posteriormente genere el archivo correspondiente. Para el primero de los casos, Oruxmaps es probablemente la aplicación que ofrece mayor potencia, con una gran cantidad de opciones de configuración y personalización.
Una vez creada la ruta y almacenada en un formato de intercambio estándar, habitualmente GPX, puede ser compartida con otros usuarios.
Aplicaciones y webs de rutas de senderismo
Existen sitios web especializados en compartir rutas en internet donde generalmente pueden descargarse de forma gratuita como Wikiloc, Strava, Sicami Tracks o AllTrails, entre otras, aunque para obtener características avanzadas como análisis de rutas, etc., casi siempre será necesario algún tipo de suscripción de pago. Entre todas constituyen un repositorio de millones de rutas.
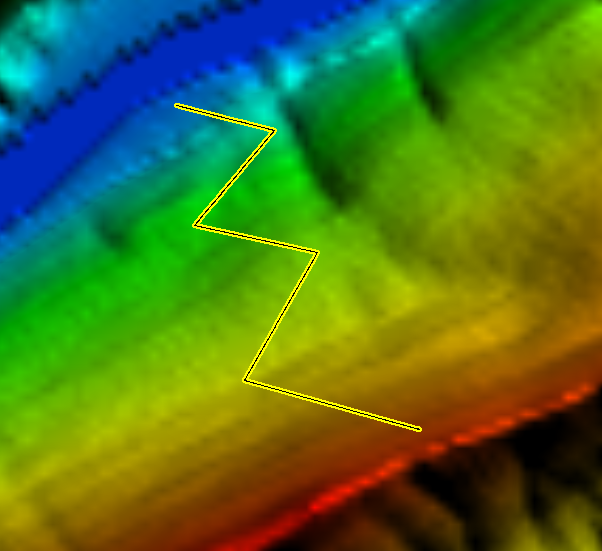
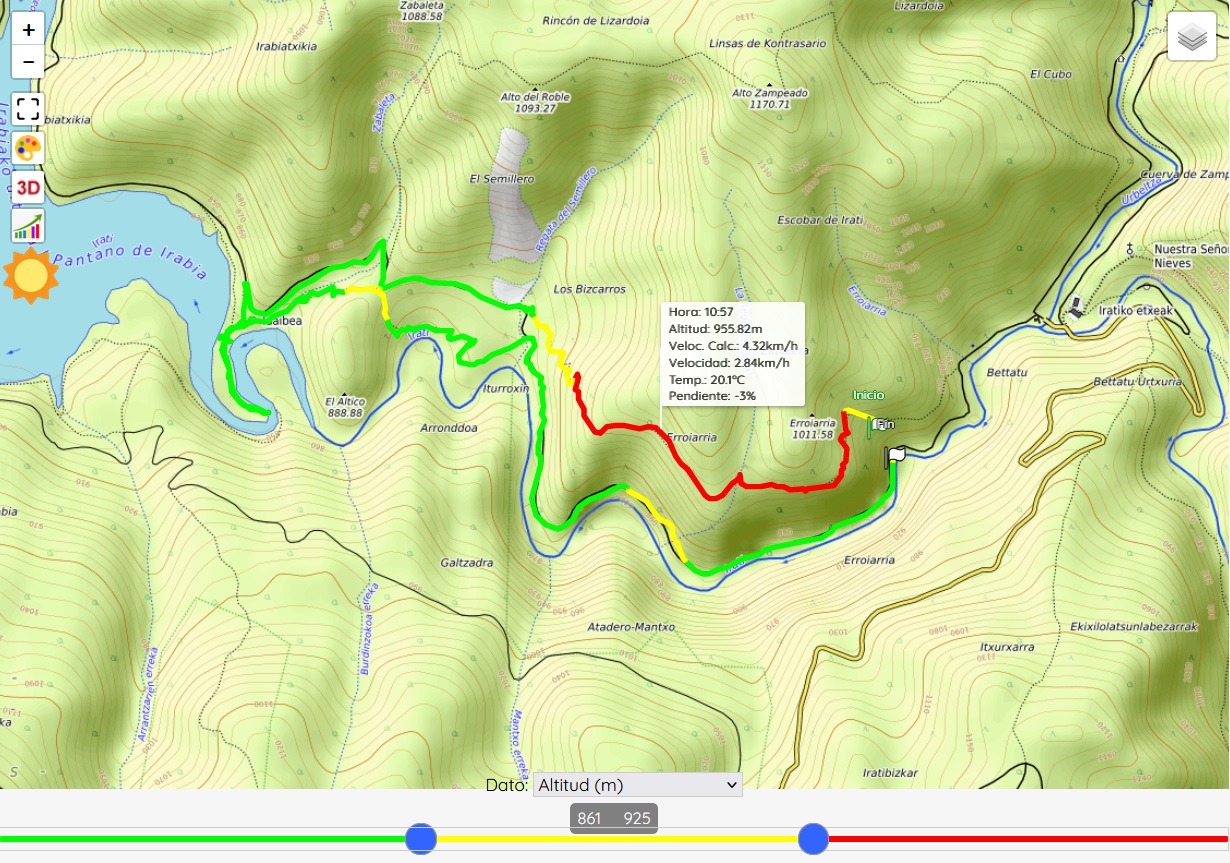
Como ejemplos de funciones adicionales, que mostramos aquí para el caso de Sicami Tracks, ya que se ofrecen bajo suscripción sin coste, podemos tener el análisis de la ruta en función de diversos parámetros, como la pendiente del terreno o la altitud:
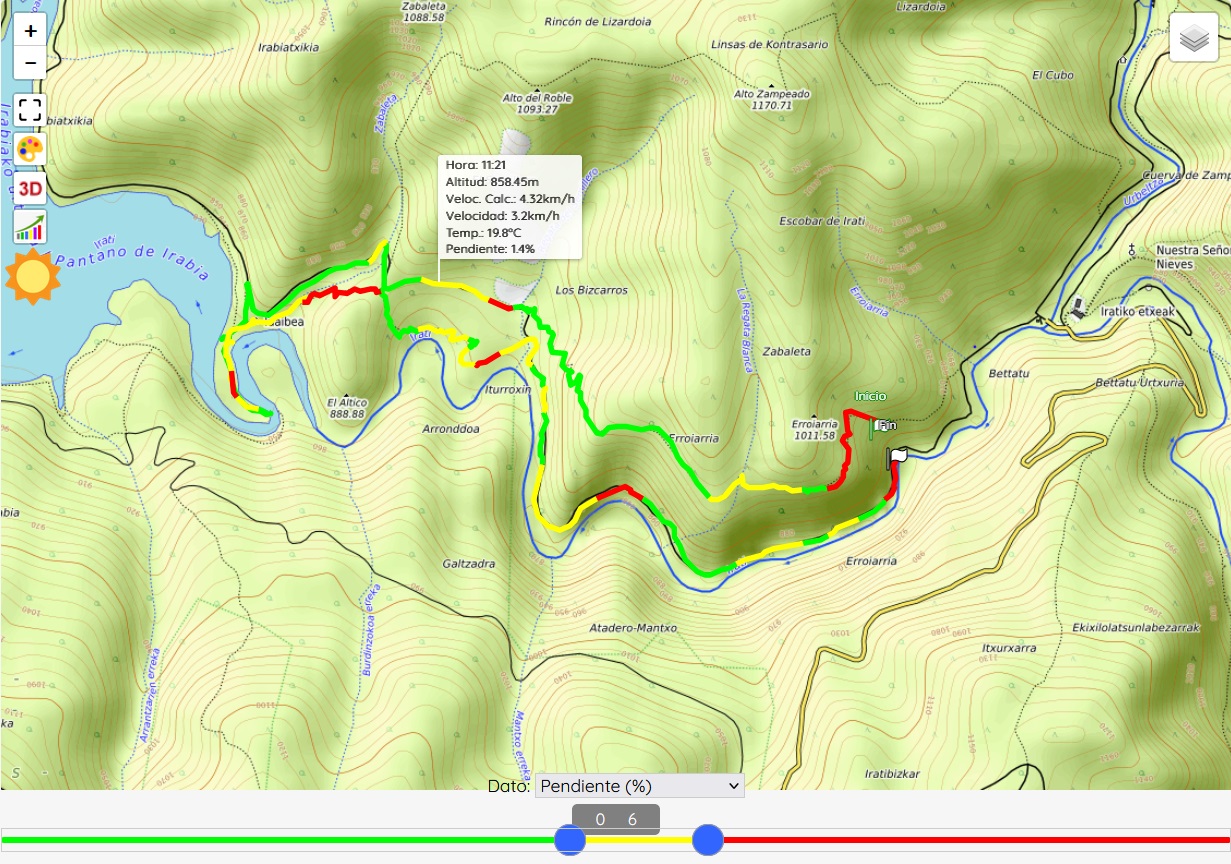
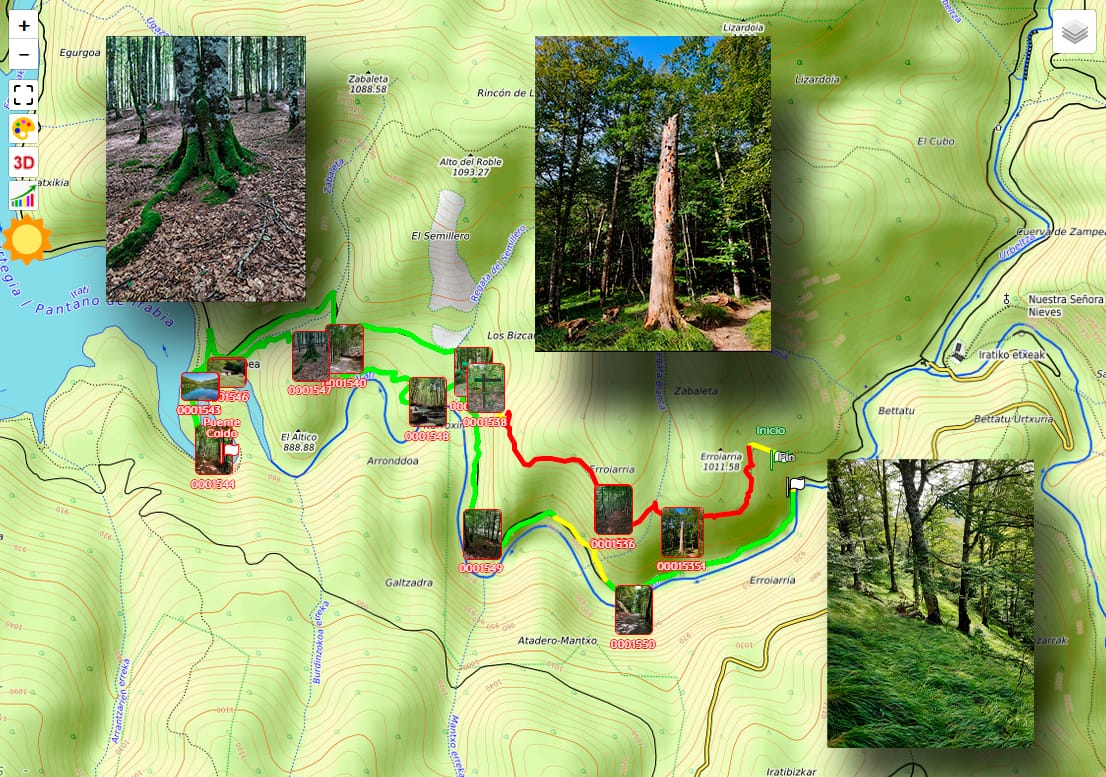
También es posible añadir puntos de ruta o "waypoints" a los que se les pueden asociar comentarios o aclaraciones e incluso elementos multimedia como fotografías o vídeos.
Incluso será posible la visualización animada del recorrido de la ruta en tres dimensiones 3D.
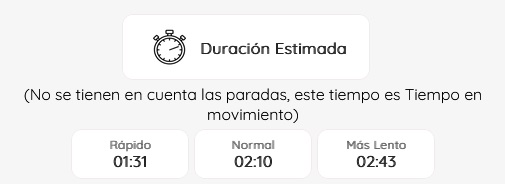
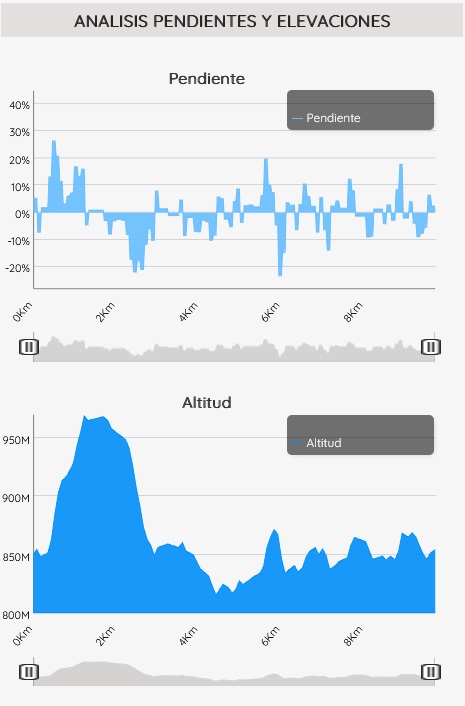
Así como otras funciones relacionadas con las características de la ruta como la duración estimada de la ruta, nivel orientativo de dificultad,


Gestión eficaz y eficiente del tiempo. Consejos y recomendaciones.
Gestión eficaz y eficiente del tiempo. Consejos y recomendaciones.

No gestionar bien el tiempo puede tener consecuencias en diferentes ámbitos de nuestra vida:
- En nuestra salud: el estrés o la ansiedad es un factor de riesgo para la aparición de algunas enfermedades, trastornos cardiovasculares o digestivos. También afecta a nuestra la salud mental, pudiendo provocar trastornos de ansiedad, adicciones, depresión, etc. La ausencia de descansos (que deben estar incluidos en el planning de organización del tiempo) es una de las causas más comunes para que la falta de tiempo acabe repercutiendo en la salud.
- En nuestro trabajo: la reducción del rendimiento, el estrés laboral, el burnout (estar quemado), la incapacidad para asumir tareas interesantes por no tener tiempo para ello, o la pérdida de objetivos.
- En nuestra vida personal: amigos, pareja, familia...
Por otro lado, las causas que originan una mala gestión del tiempo pueden ser:
- Actitud personal
- Plantearse objetivos demasiado ambiciosos que consumen una gran cantidad de tiempo.
- Mala asignación de tiempo a las tareas.
- Irregularidad a la hora de seguir los pasos para cumplir un objetivo.
- No saber decir "no" o no saber delegar tareas.
- Falta de objetivos claros o no tenerlos correctamente definidos.
- Ausencia de prioridades que nos lleva a mantener una actividad intensa pero descontrolada.
Recomendaciones generales y tips.
- Plantearse unos objetivos que marquen el camino a seguir: no perderse y dar vueltas sin rumbo, esto desgasta enormemente. Para que los objetivos sean útiles deben ser medibles, alcanzables, realistas, específicos y ajustables.
- A lo largo de unos días, hacer un estudio sobre a qué dedicamos el tiempo: registrar todo lo que hacemos y el tiempo que le dedicamos. De esta manera descubriremos si es posible optimizar nuestro tiempo e incrementar nuestro rendimiento.
- Analizar las tareas o acciones repetitivas para ver la posibilidad de optimizarlas o incluso eliminarlas. Identificar los cuellos de botella.
- Usa la agenda y las listas de tareas: improvisar no está mal, pero para organizar el tiempo no es lo más recomendable. Intenta planificar las semanas incluyendo tiempo para imprevistos y para el descanso.

- Delegar las tareas: a veces uno no puede hacerlo todo. Si es posible, debemos apoyarnos en personas que ofrecen su ayuda o que creemos que pueden encargarse de aquello que no es totalmente imprescindible hacer por uno mismo.
- Dar instrucciones por escrito al personal delegado esto evitará tener que tener que reiterarlas.
- Aprender a decir no: para no encontrarnos atendiendo tareas de otros, menos relevantes y poder esforzarnos por lo importante (lo que va dirigido a nuestros objetivos) y no tanto por lo urgente.
- Dejar las exigencias y perfeccionismos para momentos donde tengamos más disponibilidad y calma. Tenemos que hacerlo lo mejor posible, pero siempre dentro del plazo disponible.
- Intentar no distraerse con cosas que se pueden hacer en otro momento o que, si lo pensamos bien, no son tan importantes y entorpecen que alcancemos nuestros objetivos.
- Establecer mecanismos para gestiónar las posibles "perturbaciones" en el tiempo que puedan aparecer.
- Reservar tiempo para imprevistos y cambios.
- Planificar: gestionar la planificación del conjunto de actividades profesionales y personales.
- Establecer horarios de trabajo y resto de actividades que sean realistas, contemplando actividades de ocio y extralaborales en general.
- Desarrollar la capacidad de ser flexible en la modificación de la planificación.
- Organizar correctamente los documentos, el lugar de trabajo, las herramientas, la ropa, los útiles...
- Desde el punto de vista meramente laboral, no es mejor trabajador el que dedica más horas al trabajo, si no el que hace más cosas útiles en las mismas horas (PRODUCTIVIDAD)
Como hemos indicado anteriormente, es muy recomendable analizar la jornada para tratar de identificar los distintos periodos de tiempo en que podemos dividirla atendiendo al nivel de actividad, nivel de calma y nuestras propias capacidades. Algunos vendrán originados o estarán condicionados por agentes externos como periodos de mayor actividad por visitas, llamadas, etc. o de mayor tranquilidad por la ausencia de éstas. En otros casos los originarán o condicionarán agentes internos como pueden ser los horarios del personal o la capacidad de trabajo propia.
Por lo tanto, con objeto de distribuir las actividades y adaptar nuestras capacidades a los diferentes periodos de tiempo, deberíamos también analizar cuales son nuestras propias capacidades personales, nuestra respuesta en cada momento de la jornada. Nuestro momento de mayor y menor energía, y nuestra respuesta ante diferentes circunstancias.
Una vez identificadas y clasificadas las tareas, estableciendo importancia, urgencia y necesidad de recursos y tiempo a emplear en cada una de ellas, podremos organizar el tiempo disponible en función de los periodos de actividad, de nuestras propias capacidades y ayudándonos de herramientas como la lista de tareas y de la matriz de Eisenhower.

Gestionar eficazmente el tiempo consiste esencialmente en adquirir las capacidades y habilidades necesarias para planificar el tiempo adecuadamente, con el objetivo de mejorar nuestra eficiencia en los diferentes ámbitos de nuestra vida (laboral, familiar, social, personal, etcétera).
Artículo recomendado: Gestión eficaz y eficiente del tiempo. Matriz de Eisenhower
Gestión eficaz y eficiente del tiempo. Matriz de Eisenhower, Stephen, Covey.
Gestión eficaz y eficiente del tiempo. Conceptos.
Eficacia: Conseguir cumplir un objetivo en el tiempo señalado (o en menor tiempo), sin importar los recursos empleados.
Eficiencia: Alcanzar la meta empleando los mínimos recursos posibles, entre ellos el tiempo.
La “falta de tiempo” es uno de los principales problemas que todos sufrimos en la actualidad y también es, a menudo, una de las principales excusas para posponer nuestras salidas o entrenamientos. Compatibilizar nuestros trabajos, obligaciones familiares, tareas domésticas, etc. con nuestras actividades deportivas o al aire libre puede resultar una tarea compleja y hasta abrumadora.
Vamos a intentar que esta “guía” o relación de claves, sugerencias (tips) y consejos sirva de ayuda para conseguirlo o al menos mejorarlo.
Como la tarea que suele ocupar la mayor parte de este tiempo es el trabajo, siendo además una de las principales fuentes de estrés, vamos a enfocarlo especialmente a esta labor, aunque es válido para cualquier ámbito de la vida.
Una herramienta para la gestión del tiempo que puede resultar muy ilustrativa, dando una interesante visión de conjunto, es la matriz de Eisenhower o Sephen Covey.
En este método se van a clasificar las tareas en cuatro cuadrantes según su IMPORTANCIA y su URGENCIA.
De este modo vamos a definir tareas IMPORTANTES, NO IMPORTANTES, URGENTES y NO URGENTES.
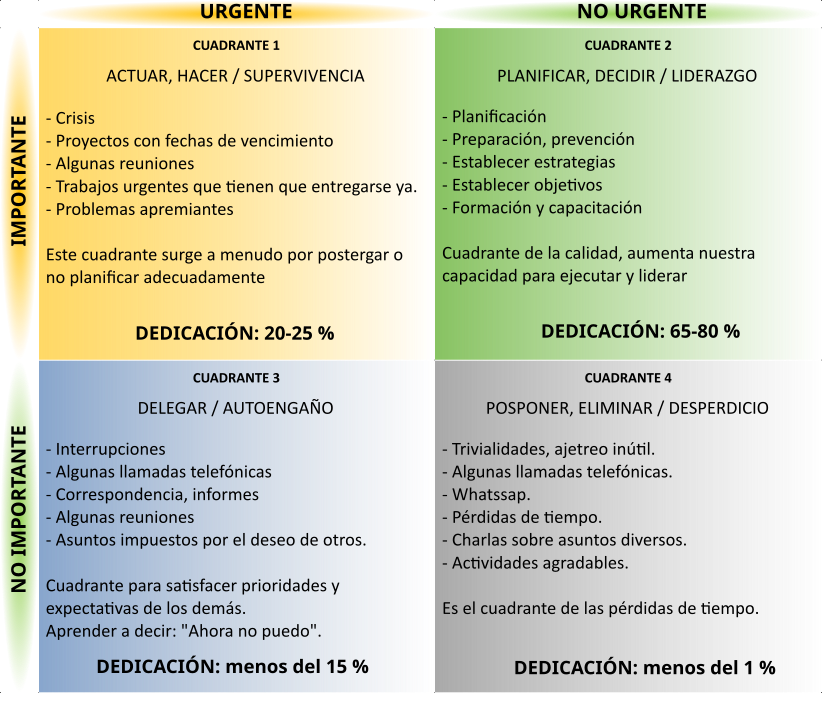
CUADRANTE 1: El cuadrante de la crisis y el estrés, debe servir solo para imprevistos, con lo que no deberíamos tener planeadas actividades en este cuadrante. Si existen, será por situaciones de crisis excepcionales, en caso contrario denota un problema de organización y de gestión. Por lo tanto, hay que minimizar las tareas en este cuadrante, lo cual se consigue trabajando correctamente el cuadrante número 2. Las tareas que realmente sean importantes y urgentes requieren de una atención inmediata y cuanto más nos demoremos en terminarlas mayor estrés y agotamiento provocarán.
Concentrarse en el cuadrante 2 minimiza el cuadrante 1.
CUADRANTE 2: El cuadrante de la planificación. Aquel al que deberíamos dedicarle mayor tiempo pues afecta a los objetivos a medio-largo plazo y su correcta gestión minimizará los imprevistos.
CUADRANTE 3: Tareas no importantes pero urgentes. Es recomendable delegarlas si es posible o automatizarlas estableciendo un sistema que permita realizarlas de la forma más óptima. El autoengaño ocurre porque las tareas de este cuadrante pueden necesitar que les dediques mucho tiempo, haciendo que te sientas muy ocupado, pero no suponen ningún avance importante.
CUADRANTE 4: Tareas que no son ni importantes ni urgentes, en cuyo caso lo mejor sería posponerlas o eliminarlas, pues suponen un desperdicio de tiempo que no permiten avance alguno.
Claves:
PROCRASTINACIÓN: Acción o hábito de retrasar actividades o situaciones que deben atenderse, sustituyéndolas por otras situaciones más irrelevantes o agradables. Procrastinar recurrentemente provocará que se dedique el mayor tiempo al cuadrante 3 y 4, ninguno al cuadrante 2 por lo que frecuentemente se encontrará en el cuadrante 1, estresado por situaciones graves que ya están fuera de control.
LISTA DE TAREAS: Relación de tareas que se deben realizar.
IMPORTANCIA: La importancia está asociada a las consecuencias que tendremos. Algo es más o menos importante según la gravedad de lo que nos pasará si no lo hacemos.
URGENCIA: La urgencia está asociada al tiempo. Aumenta por la fecha límite y por el tamaño de la tarea. Si dos tareas llevan el mismo tiempo hacerlas, es más urgente la que tenga fecha límite antes. Si dos tareas tienen la misma fecha límite, la más urgente es la que lleve más tiempo hacerla.
La importancia tiene más "fuerza" que la urgencia.
PRIORIZAR: Establecer la prioridad de cada tarea. Dar orden en el tiempo.
¿Quién determina importancia y urgencia?: normalmente, en el ámbito laboral, la importancia y urgencia la determina el responsable del departamento. Es conveniente no tener miedo a preguntar para tener claras las prioridades de cada tarea.
¿Qué beneficio obtengo como trabajador?: De nuevo enfocándonos al terreno laboral, gestionar bien el tiempo redundará en menos estrés, menos broncas, menos problemas, mejores resultados y mayor reconocimiento profesional.
Método:
Paso 1: Relacionar todas las tareas u objetivos a realizar sin tener en cuenta su importancia o urgencia por ahora.
Paso2: Atribuir a cada tarea su importancia, puntuando de 1 a 5, siendo 5 la máxima importancia.
SOLO LOS NUMEROS 4 Y 5 DAN URGENCIA O IMPORTANCIA MÁXIMA.
Paso3: Atribuir a cada tarea su urgencia, puntuando de 1 a 5, siendo 5 la máxima urgencia.
Paso4: Relacionar las tareas en la matriz.
SOLO LOS NUMEROS 4 Y 5 DAN URGENCIA O IMPORTANCIA MÁXIMA.
PASO 4: Relacionar las tareas en la matriz
Artículo recomendado: Gestión eficaz y eficiente del tiempo. Consejos y recomendaciones
Modelado de un terminal para cable de freno o cambio de bicicleta para impresion 3D
Creación de un modelo sencillo para impresión 3D con OpenSCAD
Vamos a realizar un ejemplo sencillo de utilización de técnicas de modelado 3D para posterior impresión 3D
Fabricaremos un terminal para cable de freno y/o cambio de bicicleta.
Para modelar utilizaremos OpenSCAD, software libre para la creación de objetos sólidos 3D ya que es de uso libre y además permite el diseño paramétrico con lo cual será posible modificar posteriormente las dimensiones para adaptar el modelo a cada necesidad particular.
Enlace de descarga OpenSCAD: https://openscad.org/
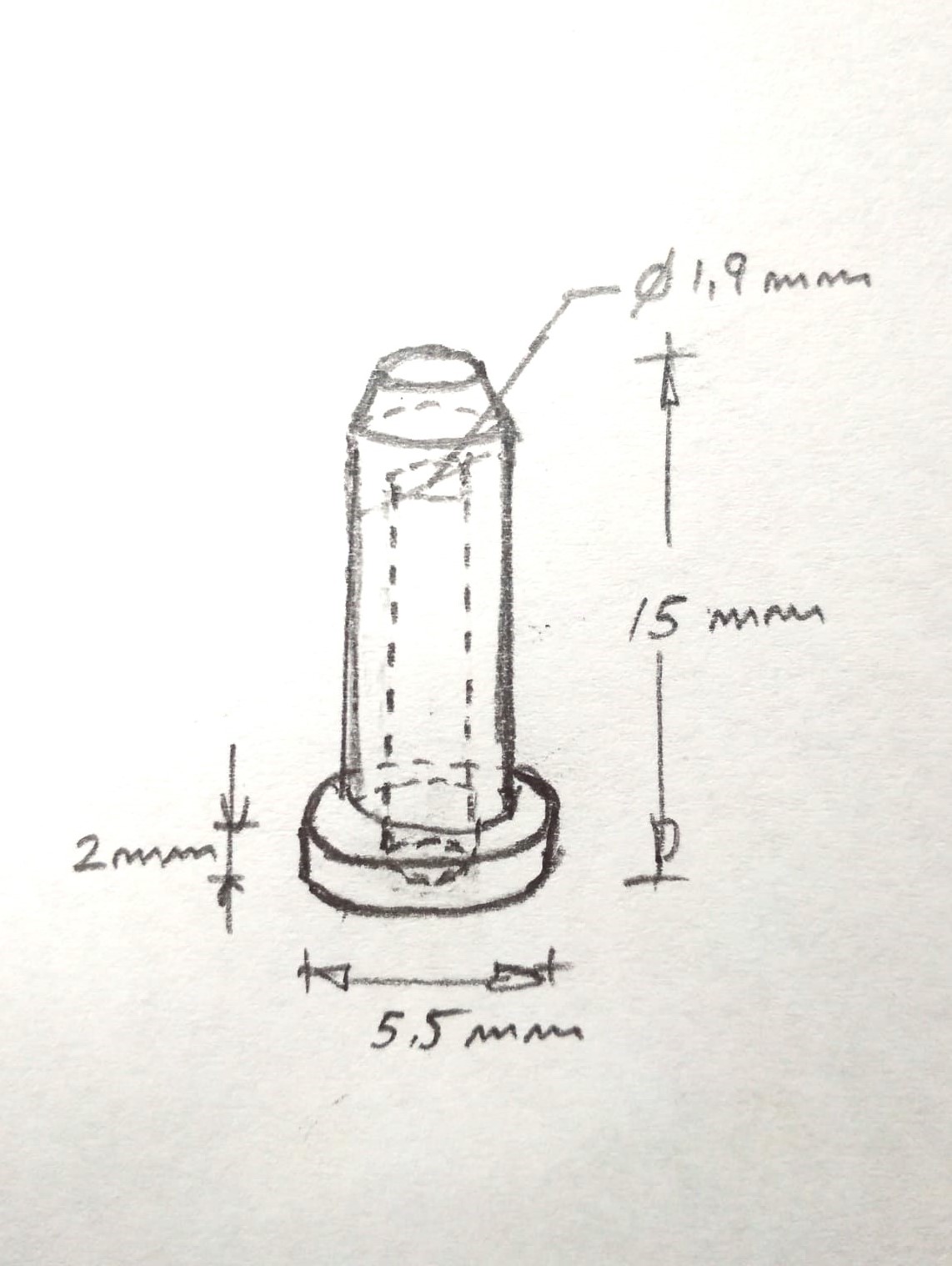
Comenzamos por elaborar un boceto que represente nuestra idea de partida
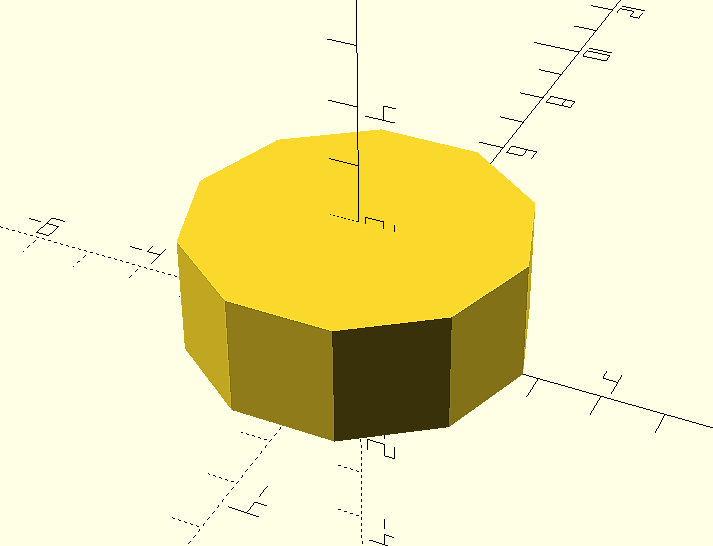
Ya en openSCAD, vamos a empezar por la base dibujando un ciclindro de diámetro 5.5 mm. y altura 2 mm.
cylinder(d=5.5, h=2, $fn=100);

El parámetro variable $fn lo utilizamos para indicar el número de segmentos que conformará el círculo base de la figura y por tanto el número de caras del cilindro. Este sería el resultado para un valor $fn = 10
Por sencillez vamos a realizar ya el taladro o perforación en este primer módulo del objeto.
El taladro será otro cilindro de la misma o mayor altura y diámetro el de la perforación:
cylinder(d=1.9, h=3, $fn=100);
En la siguiente figura está representado en color rojo y con altura 3 mm. para mejor visualización.

Pero ahora lo que te tenemos son dos cilindros superpuestos, para que el segundo cilindro sea la perforación del primero utilizaremos el modificador “difference()” que realizará la diferencia entre el primer y segundo elementos indicados:
difference(){
cylinder(d=5.5, h=2, $fn=100);
cylinder(d=1.9, h=3, $fn=100);
}

Vamos a crear el segundo cilindro o cuerpo principal del objeto, su diámetro será de 4 mm. y su longitud de 13 mm.
cylinder(d=4, h=13, $fn=1000);
Para que su posición inicial coincida con la cara superior del cilindro base lo desplazaremos 2 mm según el eje vertical “Z” utilizando la transformación “translate ([x, y, z])” quedando:
translate ([0, 0, 2])
cylinder(d=4, h=13, $fn=1000);
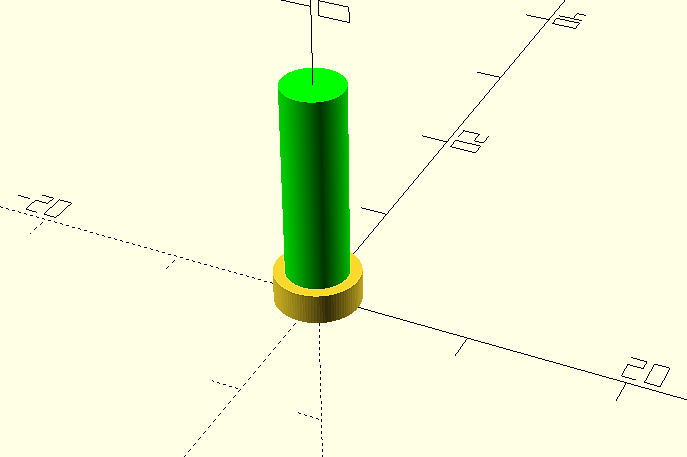
Realizaremos el taladro del modo que vimos anteriormente, aunque en este caso no queremos que atraviese toda su longitud por lo que su longitud será menor en 1 milímetro.
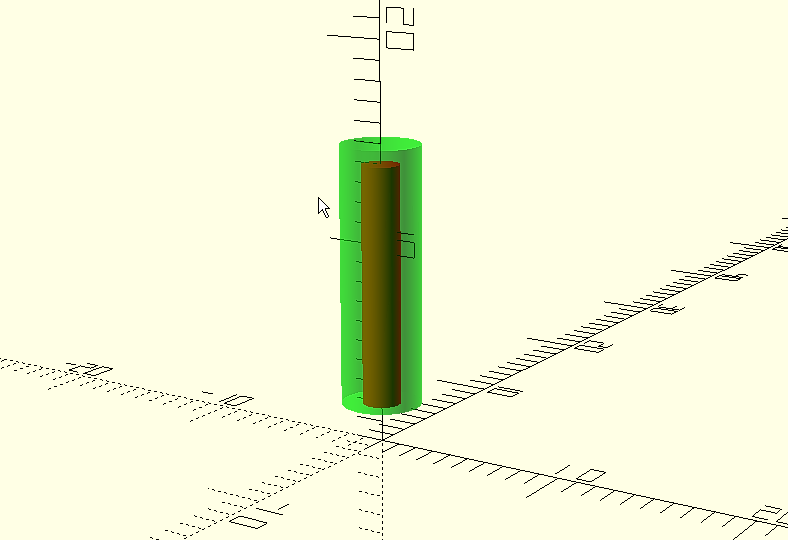
difference(){
translate([0,0,2]);
cylinder(d=4, h=13, $fn=1000);
cylinder(d=1.9, h=12, $fn=1000);
}
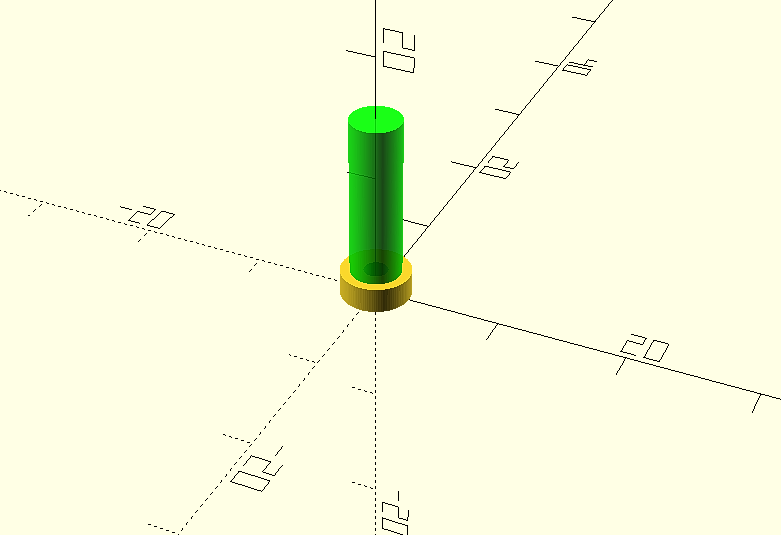
Ya solamente nos quedaría el achaflanado superior. En este caso lo haremos como un tercer elemento, otra vez utilizaremos un cilindro, pero definiremos un diámetro menor para la cara superior. Utilizaremos de nuevo la primitiva “cylinder” para crear un cilindro de altura h=1, diámetro inferior d1=4 y diámetro superior d2 =2.
cylinder(h=1, d1=4, d2 = 2, $fn=100);
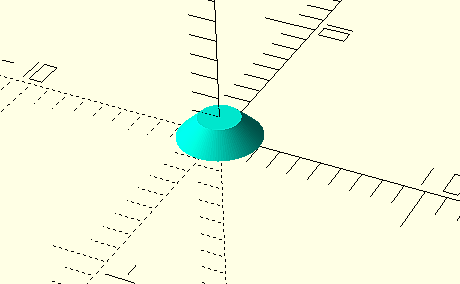
Y de nuevo lo desplazamos hasta su posición correcta en el extremo superior del terminal
translate([0,0,15]);
cylinder(h=1, d1=4, d2 = 2, $fn=100);
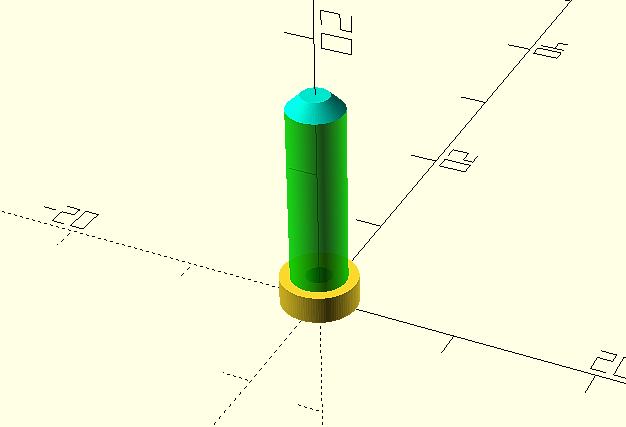
El resultado final, incluido el código completo será:
difference(){
cylinder(d=5.5, h=2, $fn=100);
cylinder(d=1.9, h=3, $fn=100);
}
difference(){
translate([0,0,2])
cylinder(d=4, h=13, $fn=1000);
cylinder(d=1.9, h=12, $fn=1000);
}
translate([0,0,15])
cylinder(h=1, d1=4, d2 = 2, $fn=100);
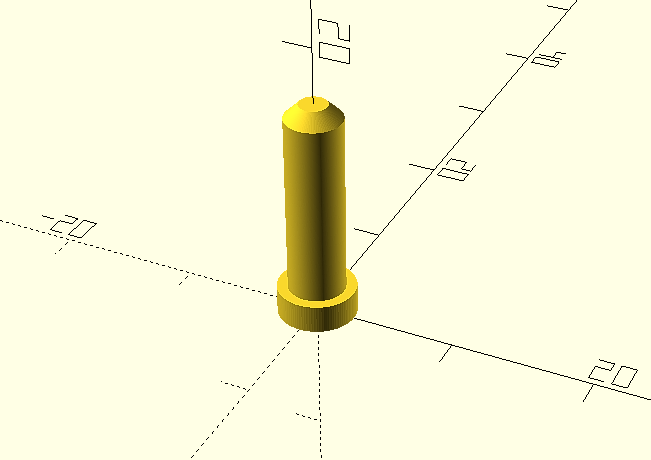

A continuación lo renderizaremos (F6) y lo exportaremos para la impresión 3D, en nuestro caso en formato .STL Y este será el resultado final una vez impreso.

Eratóstenes de Cirene. Cálculo del radio de la Tierra.
Eratóstenes de Cirene (276 a.C - 194 a.C.). El radio de la Tierra
Eratóstenes fue un matemático, astrónomo y geógrafo, nacido en el año 276 a. C. en Cirene, antigua ciudad griega en la actual Libia, conocido, entre otras aportaciones, por su trabajo en la estimación del radio de la tierra.
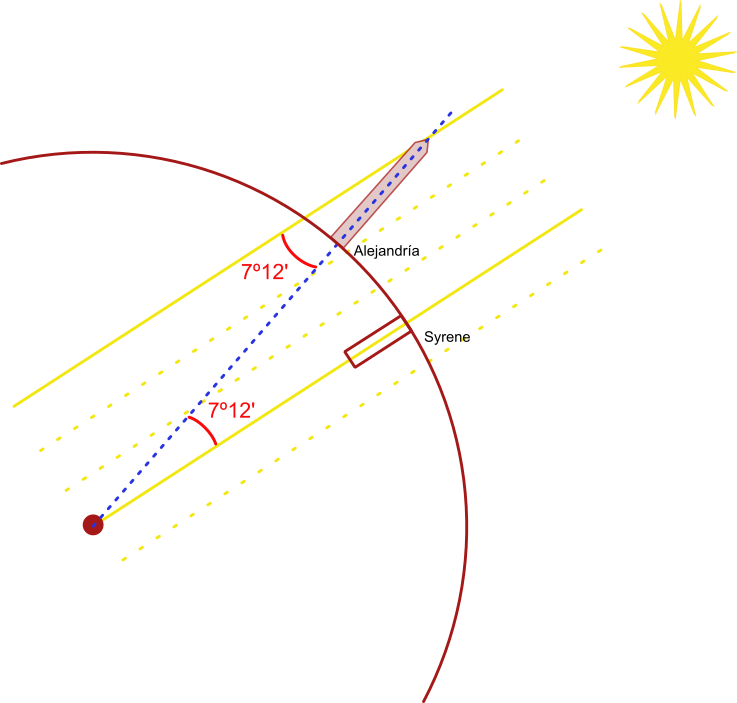
Siendo director de la Biblioteca de Alejandría (Egipto) fue conocedor de observaciones que indicaban que en Syene, actualmente Asuán, al mediodía del solsticio de verano (momento en el que el Sol alcanza su posición más elevada en el cielo) se observaba que los objetos no proyectaban ninguna sombra y la luz entraba en los pozos hasta lo más profundo. Esto significaba que los rayos del sol caían perpendiculares sobre la tierra en esa zona.
En Alejandría, en ese mismo día, los cuerpos sí que producían sombras. Es decir, que esos mismos rayos de sol no caían perpendiculares, si no formando cierto ángulo.
Hay que indicar que Eratóstenes ya sostenía que la tierra era curva por lo que esta diferencia en el ángulo de incidencia de los rayos del sol reforzaba su creencia.
También creía que el sol estaba lo suficientemente lejos como para considerar que sus rayos alcanzarían la tierra prácticamente paralelos entre sí.
Además, si el sol entraba en el pozo hasta el fondo, podía inferir que, si se prolongaban, llegarían al centro de la tierra.
La distancia entre Alejandría y Syene era de alrededor de 5.000 estadios, medida utilizada en la época que, aunque no se conoce con exactitud, se estima que equivale a unos 158 metros.
Eratóstenes fue capaz de medir cual era el ángulo con el que esos rayos de sol incidían en Alejandría y el resultado fue de aproximadamente 7º 12’. No se conoce el método que empleó para obtenerlo. .
Conociendo que la circunferencia completa comprende 360º, Eratóstenes dividió por los 7.2º medidos, resultando que es aproximadamente unas 50 veces la circunferencia:
360 / 7.12 = 50
de donde infirió que la circunferencia de la Tierra debía ser unas 50 veces la distancia entre Alejandría y Siena, es decir 50 x 5000 = 250.000 estadios.
Si tenemos en cuenta el valor estimado en metros para un estadio tendremos que la circunferencia de la tierra sería de:
250.000 estadios x 158 metros/estadio = 39.500.000 metros = 39.500 km
Para aquella época Arquímedes ya había realizado un cálculo aproximado para el valor de PI estableciéndolo en 22/7 y era conocida la relación entre la longitud de una circunferencia y su radio:
Despejando el radio en la fórmula anterior:
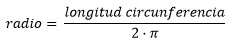
Utilizando los valores obtenidos por Eratóstenes:
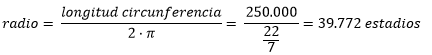
Si damos por válidos los 158 metros que se supone que medía cada estadio:
39.772 · 158 = 6.283.976 metros = 6.284 km.
La Tierra no es perfectamente esférica, por lo que no tiene sentido hablar de un radio único, podemos encontrar que el radio en el ecuador es de 6.378 km mientras que el radio polar es de 6.357 km. Cómo referencia se considera 6.371 km el radio medio en un modelado esférico de la Tierra.
Esto es un ejemplo de aplicación de geometría básica y de que las civilizaciones antiguas no necesariamente eran primitivas intelectualmente.
Sistemas de referencia de coordenadas. Datum. Conceptos básicos.
Sistemas de referencia de coordenadas. Datum. Conceptos básicos.
El Datum es un sistema de referencia geodésico que se compone de un elipsoide, en el que se ha establecido un sistema de coordenadas que permita la localización de cualquier punto sobre su superficie y su posición en relación a la Tierra.
Punto fundamental
Para poder establecer este sistema de referencia de coordenadas es necesario establecer previamente una relación clara entre las posiciones relativas entre el elipsoide y el geoide de manera que el elipsoide se ajuste lo mejor posible a la región donde se utilizará. Para ello es necesario definir un punto común a ambos, donde ambos coincidan y que será un punto tangente al elipsoide y al geoide. A este punto se le denomina “punto fundamental”. El punto fundamental quedará definido por sus coordenadas geográficas de longitud y latitud.
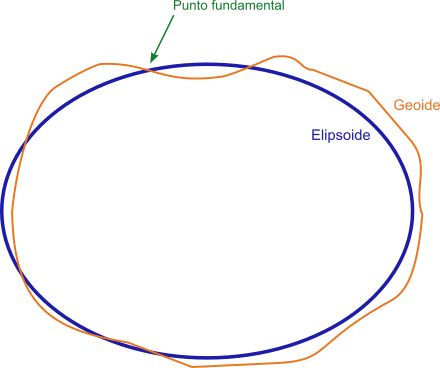
Cuando comenzaron a elaborarse los Datums, debido a que las técnicas existentes para las mediciones necesitaban apoyarse sobre el terreno, los diferentes países o regiones buscaron puntos locales según sus zonas de influencia para definir el punto fundamental de su Datum, haciendo coincidir la superficie del geoide y del elipsoide, desplazando así el elipsoide según conveniencia. Esto ha provocado que existan diferentes datums para diferentes regiones. Progresivamente se ha ido llegado a acuerdos regionales para la adopción de sistemas de referencia comunes que ampliaron la cobertura geográfica de estos datums locales.
En la actualidad, los sistemas satelitales han permitido elaborar datums globales, donde lo habitual es que el origen de coordenadas se establezca en el centro de masas de la Tierra.
Datums locales o regionales y Datums globales
Por lo tanto, podemos distinguir entre Datums locales o regionales y Datums globales.
Datums locales
En los datums locales se define un origen y situación de un sistema de coordenadas válido para una determinada zona de la Tierra, aunque no para toda ella y se compone del elipsoide definido por sus ejes e índice de aplastamiento y por su “punto fundamental”.
Datums globales
En los Datums globales el centro geométrico del elipsoide coincide habitualmente con el centro de masas de la Tierra y no existe un “punto fundamental” como tal.
Un ejemplo de datum local sería el datum europeo ED 50 que emplea el Elipsoide Hayford con semieje mayor a = 6.378.388 metros y aplanamiento f = 1 / 297. Su origen para las longitudes es el meridiano de Greenwich y su Punto Fundamental está situado en Postdam (Alemania) en las coordenadas 52º22’51.446”N 13º03’58.741”E
Como ejemplo de datum global tendríamos el WGS84 que emplea el Elipsoide GRS_1980 con semieje mayor a = 6.378.137 metros y aplanamiento f = 1 / 298,25722356300003. Su origen de longitudes es el meridiano de Greenwich y no tiene punto fundamental al ser global.
Datum WGS84
Los sistemas GPS utilizan internamente el Datum WGS84 por lo que es conveniente configurar el Datum del dispositivo según la cartografía que estemos utilizando. El dispositivo se encargará de realizar las conversiones oportunas para que las coordenadas de cada punto coincidan sobre el mapa. Del mismo modo, los tracks en formato GPX que se generen mediante un dispositivo GPS siempre almacenarán las coordenadas conforme al Datum WGS84.
Datums verticales
Al igual que en el caso del Datum para coordenadas horizontales, en el caso de los sistemas de coordenadas verticales se establece un Datum vertical que será la superficie que se tomará como referencia con elevación o altitud cero. En la práctica normalmente se utilizarán datos de mediciones y cálculos almacenados en ficheros raster de elevaciones.
Altitud ortométrica y altitud elipsoidal
Las dos superficies que se emplearán serán el elipsoide y el geoide lo cual da lugar a dos definiciones de altitud o altura:
Altitud o altura ortométrica: Cuando la superficie de referencia es el geoide, equivalente a la altitud sobre el nivel medio del mar. La altura ortométrica será la distancia que exista entre el punto del terreno y el geoide en la dirección de la gravedad o “línea de plomada”. Esta distancia puede ser positiva o negativa según el punto esté por encima o por debajo de la superficie del geoide de referencia. Son utilizadas habitualmente para la elaboración de cartografía topográfica.
Altitud o altura elipsoidal: Cuando la superficie de referencia es el elipsoide. La altura elipsoidal será la distancia que exista entre el punto del terreno y una línea perpendicular al elipsoide. Esta distancia puede ser positiva o negativa según el punto esté por encima o por debajo de la superficie del elipsoide de referencia. Este modelo es el que emplean los sistemas GPS.
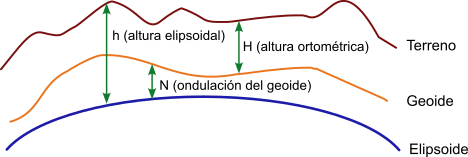
Relación entre la altitud ortométrica y elipsoidal
Si se dispone de los datos relativos a la ondulación del geoide en determinada zona, es posible obtener la altura ortométrica aproximada a partir de la altura elipsoidal aplicando la siguiente relación:
Ondulación del geoide = altura elipsoidal – altura ortométrica,
N = h - H
de donde:
Altura ortométrica = altura elipsoidal - ondulación del geoide,
H = h - N
Sistemas de referencia de coordenadas. Elipsoide y geoide.
Sistemas de referencia de coordenadas. Elipsoide y geoide. Conceptos básicos.
Para la representación de un dato geográfico es necesario disponer de una referencia espacial que lo posicione sobre la superficie de la Tierra, es decir, de un sistema de referencia de coordenadas. Estos datos geográficos en la actualidad están en forma de fichero digital, según dos modelos, el modelo vectorial que está compuesto por puntos, líneas y polígonos y el modelo raster, que consiste en celdas de una matriz o “grid”.
El modelo vectorial es apropiado para objetos o fenómenos discretos y con límites claros (parcelas, edificios, catastro, etc), mientras que el modelo raster o de estructura matricial, al permitir que cada unidad de la matriz tenga asignado un valor diferente, es más apropiado para variables cuantitativas, como temperaturas, precipitaciones, etc. que varíen según la posición x e y, así como en la posición vertical.
Sea cual sea el modelo, éste debe incorporar un sistema de referencia de coordenadas tanto horizontales como verticales, indicando la posición vertical respecto a algún sistema de referencia.
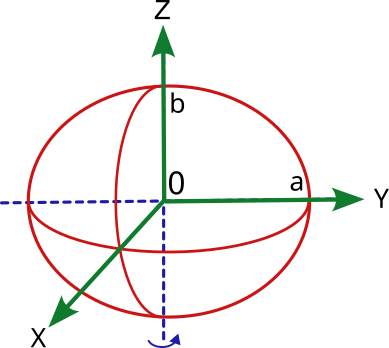
Forma de la Tierra, el elipsoide.
La forma de la tierra es aproximadamente esférica. Aunque se acepta mayoritariamente que la forma geométrica regular que mejor se ajusta a la forma real es el elipsoide de revolución.
Un elipsoide de revolución se genera cuando se hace rotar en el espacio una elipse alrededor de uno de sus ejes. La elipse queda definida por dos ejes, uno horizontal "a", otro vertical "b" y un índice de aplanamiento "f" siendo: f = (a-b)/a
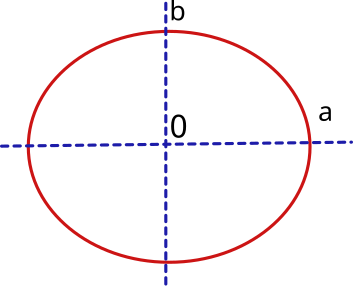
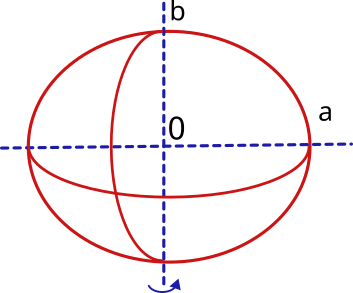
Por tanto, para definir el elipsoide terráqueo será necesario conocer su semieje mayor, que corresponderá al radio ecuatorial (en el ecuador) y su semieje menor, que corresponderá al radio polar (de centro a polos norte y sur). Además, será necesario conocer el índice de aplanamiento o achatamiento.
El modelo de elipsoide será el que servirá como base para los sistemas de referencia de coordenadas horizontales.
Forma de la Tierra, el geoide.
Pero desde el punto de vista geométrico, la forma real de la Tierra no es regular. Como tampoco lo es la distribución de las masas y materiales en su interior. Si tomamos como referencia el potencial gravimétrico de cada punto de la superficie, obtendremos una figura irregular llamada geoide.
El geoide es una superficie teórica de igual potencial (equipotencial) del campo gravitatorio de la tierra, que coincide aproximadamente con el nivel medio del mar y que une todos los puntos que tienen el mismo potencial gravimétrico, es decir que son atraídos con la misma intensidad gravitatoria hacia el centro de la tierra. Se parte del nivel medio de los océanos y mediante diferentes técnicas se obtienen valores de igual potencial gravimétrico en las zonas emergidas.

Relación entre el elipsoide y el geoide. Altura elipsoidal, altura ortométrica y ondulación geoidal
Para definir el geoide se compara su superficie con la del elipsoide regular, obteniendo la diferencia para cada punto de la Tierra. Esta información se suele almacenar en ficheros rasters.
A la diferencia de altura en cualquier punto entre la altura del elipsoide y la altura del geoide se la conoce como altura ortométrica y a la variación entre el geoide y el elipsoide se la conoce como ondulación del geoidal.

h = distancia vertical entre el punto del terreno y el elipsoide o altura elipsoidal
H = distancia vertical entre el punto del terreno y el geoide o altura ortométrica
N = distancia vertical entre el geoide y el elipsoide u ondulación geoidal
Si dijimos anteriormente que el elipsoide sería la base para los sistemas de referencia de coordenadas horizontales, el Geoide será la base para los sistemas de referencia de coordenadas verticales
Las posiciones calculadas por los dispositivos GPS son de tipo elipsoidal y el sistema de referencia asociado, conocido como World Geodetic System WGS, se refiere a un elipsoide global de referencia que se estableció por primera vez en 1960 y ha sido mejorado en ocasiones posteriores, siendo la versión actual la WGS84, definida en el año 1984.
Artículo recomendado: Sistemas de coordenadas horizontales y verticales. Datum
Potencia y energía en el ciclismo. Un cálculo práctico.
Potencia en el ciclismo. Cálculo práctico
Tal como veíamos en el artículo "Energía, trabajo y potencia", podemos definir la potencia como la cantidad de trabajo o uso de energía que efectuamos en un determinado tiempo. Es la velocidad en la realización de un trabajo o en el uso de la energía.
Por lo tanto, cuando nos referimos a movimientos de traslación, la potencia se puede expresar como el producto de la fuerza por la velocidad. En movimientos de rotación podemos considerar una "potencia instantánea" en cada punto de giro que se puede definir como el producto del momento o torque de la fuerza por la velocidad angular (ángulo girado en la unidad de tiempo). La velocidad angular es equivalente a la cadencia del pedaleo expresada en valores de ángulo por segundo.
Potencia(w) = Torque (Nm) x Cadencia (rad/seg)
La equivalencia entre revoluciones por minuto, radianes por segundo y grados sexagesimales por segundo es: 1 rpm = 2·PI/60 rad/seg = 360/60 º/seg
Artículo recomendado: Energía, Trabajo y Potencia, algunas definiciones físicas
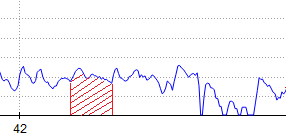
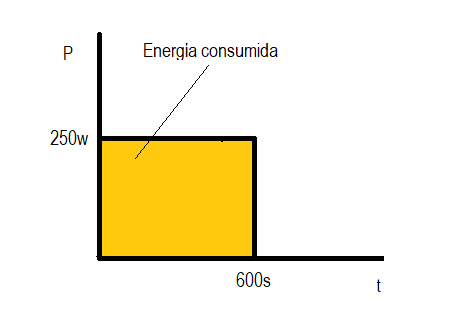
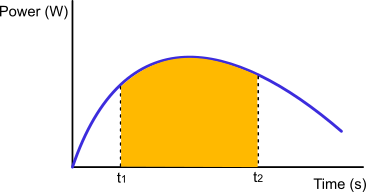
Energía consumida (Kj): Desde un punto de vista gráfico, la energía consumida al realizar un esfuerzo a una potencia determinada corresponde al área bajo la curva de potencia. Si nos referimos a la potencia desarrollada al recorrer una ruta en bicicleta, corriendo o caminando, la energía total consumida sería el área total bajo la curva de potencia desarrollada a lo largo de la ruta.
Cálculo de la energía
Ejemplo: Si tenemos a un ciclista que realiza un esfuerzo fijo de 250 vatios durante 10 minutos (600 segundos). Toda el área bajo esa curva (que es una línea horizontal en este caso) es la energía gastada para producir esa potencia.
Potencia = (Trabajo o energía) / tiempo
despejando la energía en esta fórmula,
Energía = Potencia x tiempo
y sustituyendo los valores,
Energía = 250w x 600 s = 21600 joule = 216 kj
En este caso es evidente la coincidencia con el área del rectángulo de base el tiempo (600 seg) y altura la potencia (250 w) porque al ser una potencia constante su gráfica es una línea horizontal.
Energía, Trabajo y Potencia. Definiciones físicas.
Energía, Trabajo y Potencia
La Energía, el Trabajo y la Potencia son magnitudes físicas estrechamente relacionadas entre sí.
La Energía
La Energía es la capacidad que tiene un sistema para producir un trabajo. Un sistema que tenga una cierta energía no realizará ningún trabajo hasta que esa capacidad se convierta en movimiento. Por ejemplo, una manzana en un árbol tiene una energía potencial, pero no realiza ningún trabajo hasta que no caiga.
Su unidad en el sistema internacional es el Joule (julio) que es el trabajo realizado por una fuerza de un newton cuyo punto de aplicación se desplaza en un metro en su misma dirección.
El trabajo
El Trabajo consiste en una transferencia de energía entre sistemas. En el caso de una fuerza que actúe sobre un cuerpo, su trabajo equivaldrá a la energía necesaria para desplazarlo. Se dice entonces que una fuerza que actúa sobre un cuerpo realiza un trabajo cuando provoca un desplazamiento del cuerpo en la dirección de la fuerza. Por tanto, en un sistema mecánico, si no existe desplazamiento el trabajo es nulo. Esta conclusión no es válida para sistemas termodinámicos, donde las transferencias de calor son consideradas transferencias de energía.

Solo se considera que realiza trabajo la componente de la fuerza que actúa en la dirección del desplazamiento, en el caso de la figura anterior sería la componente horizontal de la fuerza F.
El trabajo tiene las mismas unidades que la energía.
La potencia
Podemos definir la potencia como la cantidad de trabajo o uso de energía que efectuamos en un determinado tiempo. Es la velocidad en la realización de un trabajo o en el uso de la energía.
Unidades: vatios (watt).
Se genera un vatio de potencia cuando se realiza un trabajo que consume 1 Joule de energía durante 1 segundo de tiempo. 1 w = 1 joule/ 1 segundo
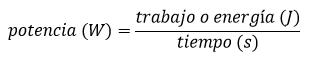
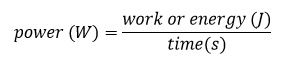
Interpretación gráfica de la energía en la gráfica de potencia
Gráficamente, la energía es el área bajo la gráfica de potencia en función del tiempo:
La Isla Nula (Null Island). Estación 13010. El origen de coordenadas. Punto Cero.
La Isla Nula (Null Island). Estación 13010. El origen de coordenadas. Punto Cero
En la intersección entre el ecuador y el meridiano de Greenwich se encuentran las coordenadas 0ºN, 0ºE. Este punto geográfico se sitúa en el Golfo de Guinea en el océano Atlántico y lo que hay en esa posición, anclada en esas coordenadas, es una boya meteorológica denominada “Soul bouy” o estación 13010, que forma parte de la red de boyas “Prediction and Research Moored Array in the Tropical Atlantic“ (PIRATA), dedicada a recopilar datos meteorológicos y oceanográficos para estudiar las interacciones océano-atmósfera en el Atlántico tropical.

Null Island o la Isla Nula es el nombre ficticio de una isla inexistente situada en esas coordenadas que dio lugar en su momento a múltiples bromas, incluida la existencia de una web de la República de Null Island, cuyo dominio “nullisland.com” está en venta a día de hoy.
Fuerzas al andar o correr. Física andando y en la carrera a pie.
Fuerzas al andar o correr
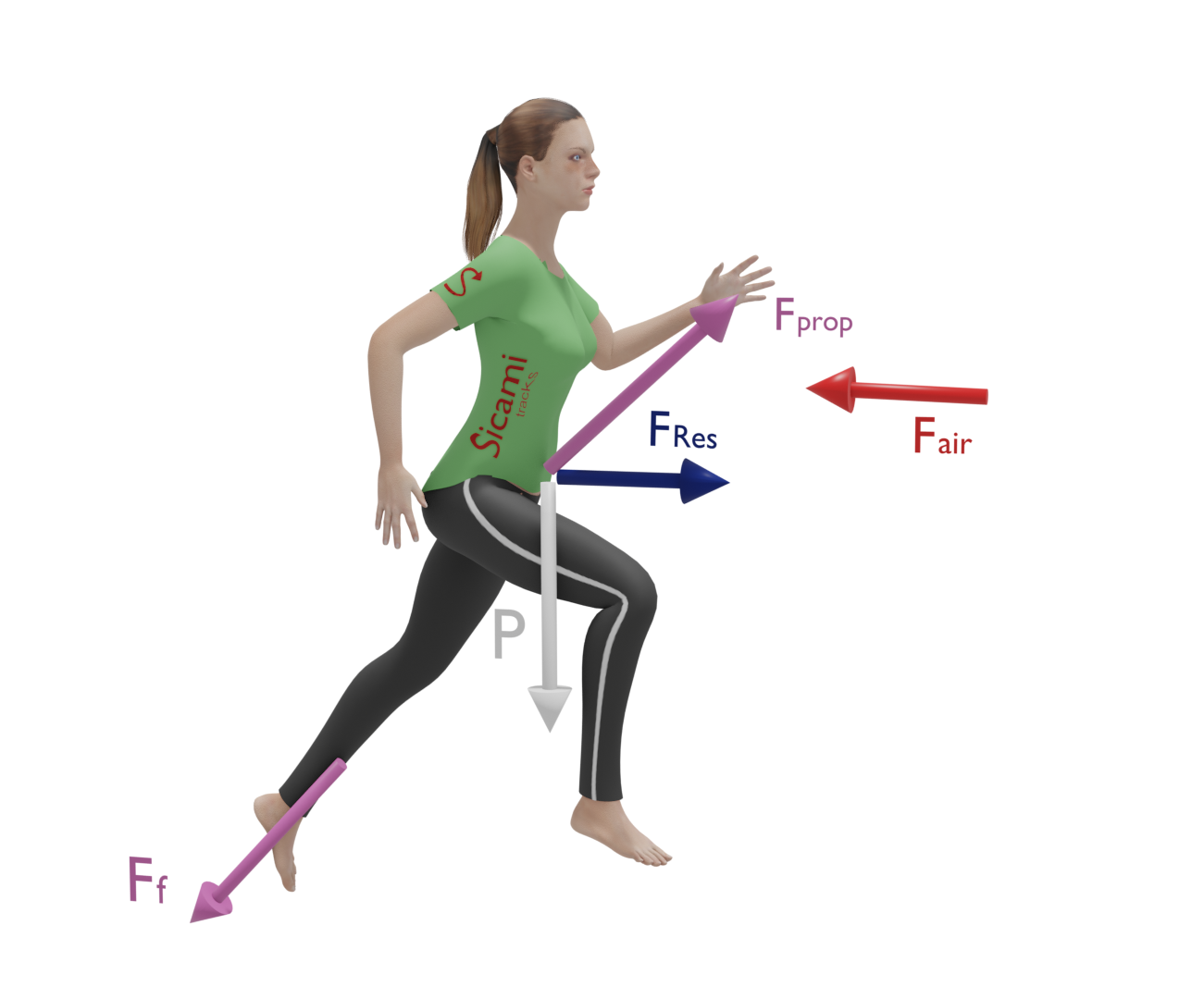
Al correr o andar aparecen muchas fuerzas en acción, la más importante, a efectos de producir el desplazamiento, es la fuerza de propulsión que ejerce el pie sobre el suelo.
Esta fuerza tiene una dirección inclinada, dependiendo del ángulo de la pisada y puede descomponerse en dos componentes en las direcciones de avance, “x” y perpendicular al suelo, “y”.
La componente “x” es la que permitirá avanzar al corredor o caminante provocando una aceleración en la dirección del avance. Esta componente será horizontal cuando nos movemos en terreno llano.
La componente “y” es la que permitirá al corredor superar la gravedad y moverse hacia arriba provocando una fuerza en dirección perpendicular al suelo.
Esencialmente la carrera consiste movimientos parabólicos consecutivos en los que el corredor empuja desde el suelo hasta alcanzar una determinada altura máxima y vuelve a aterrizar a cierta distancia por delante. En consecuencia, su movimiento puede dividirse en dos desplazamientos, uno de salto y otro de avance, y el resultado final será la consecuencia de vencer las diferentes fuerzas que se opondrán a estos desplazamientos.

La fuerza de propulsión se obtiene aplicando fuerza con el pie sobre el terreno, con el que debe existir una fuerza de fricción suficiente. La fuerza de reacción del suelo (tercera ley de Newton), es la que proporcionará la propulsión necesaria. Dicho de otro modo, al correr ejercemos una fuerza opuesta a la dirección del movimiento y según la tercera ley de Newton, el suelo ejerce sobre nosotros una fuerza igual y opuesta a nuestra fuerza sobre el suelo, lo que permite el movimiento hacia adelante.
Si no existiera la fuerza de fricción sería imposible desplazarse, sólo imagina lo que ocurre al intentar correr sobre una superficie sin fricción (por ejemplo, hielo). Si no hubiera fricción estática, el pie empujaría hacia atrás sobre la superficie y simplemente se deslizaría hacia atrás.
Vamos a ver con más detalle algunos casos particulares.
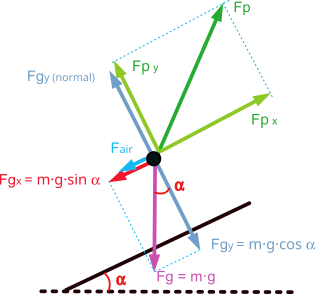
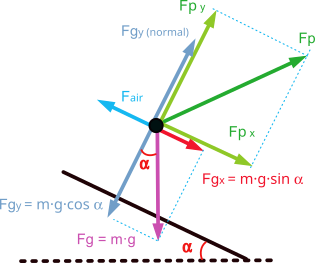
Correr en llano
En este caso, las principales fuerzas que se oponen al desplazamiento son la fuerza gravitatoria, provocada por nuestro propio peso, y la fuerza de resistencia aerodinámica provocada por el aire.
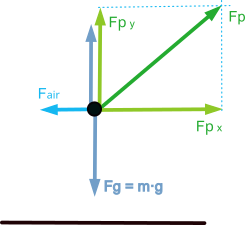
Para el movimiento de avance en llano el corredor debe aplicar una fuerza sobre el terreno que sea mayor que la suma de la fuerza de la gravedad y la fuerza de arrastre aerodinámico.
En un esquema simplificado quedaría como muestra la siguiente figura, donde se ha descompuesto la fuerza de propulsión “Fp” en una componente vertical “Fpy” que debe vencer la fuerza de la gravedad y otra horizontal “Fpx” que debe vencer la resistencia aerodinámica y proporcionar la aceleración.
Correr cuesta arriba
En este escenario aparece una componente “x” de la fuerza gravitatoria en la dirección del desplazamiento y en sentido opuesto a éste. Por otra parte vamos a observar una reducción en el valor de la fuerza de fricción.
Aunque la componente “y” (perpendicular al suelo) de la fuerza gravitatoria disminuye con la inclinación del terreno, no es suficiente para compensar el aumento de la componente “x” y la pérdida de fricción con el suelo.
##publi##
Por lo tanto, la fuerza a aplicar debe ser mayor que la suma de la fuerza de la gravedad en “x”, la fuerza de la gravedad en “y” y la fuerza de arrastre aerodinámico.
Desde el punto de vista de la energía, la carrera en ascenso no solo implica una variación en la energía cinética, si no que también se produce un incremento neto de la energía potencial.
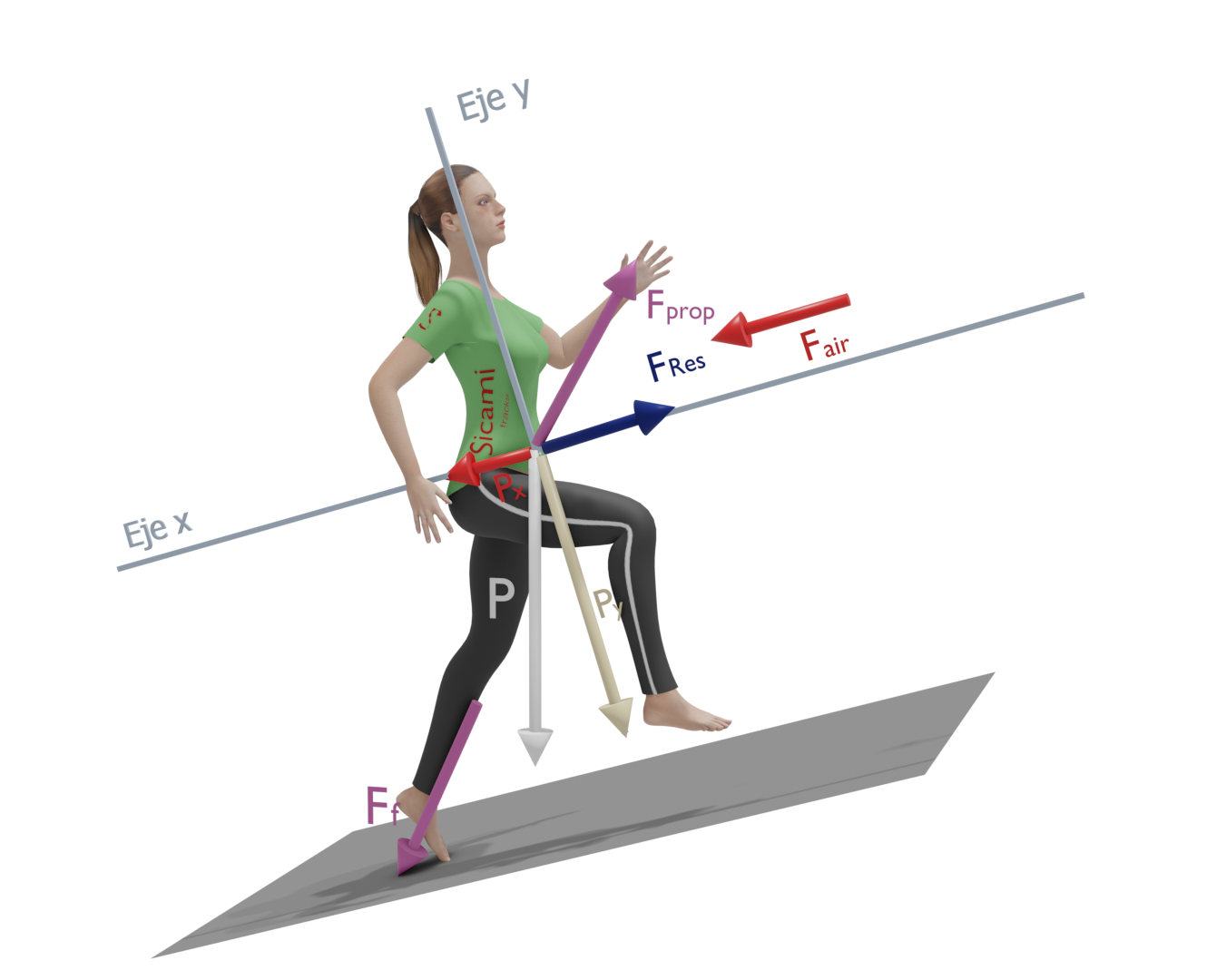
En un esquema simplificado quedaría como muestra la siguiente figura, donde se ha descompuesto la fuerza de propulsión “Fp” en una componente perpendicular al suelo “Fpy” que debe vencer la fuerza de la gravedad y otra paralela al suelo “Fpx” que debe vencer la resistencia aerodinámica, la componente “x” de la fuerza gravitatoria y, además, proporcionar la aceleración.
Correr cuesta abajo
En este caso la componente “x” de la fuerza de la gravedad será favorable al desplazamiento y las fuerzas a superar serán la de la componente “y” de la gravedad y la fuerza de arrastre aerodinámico.
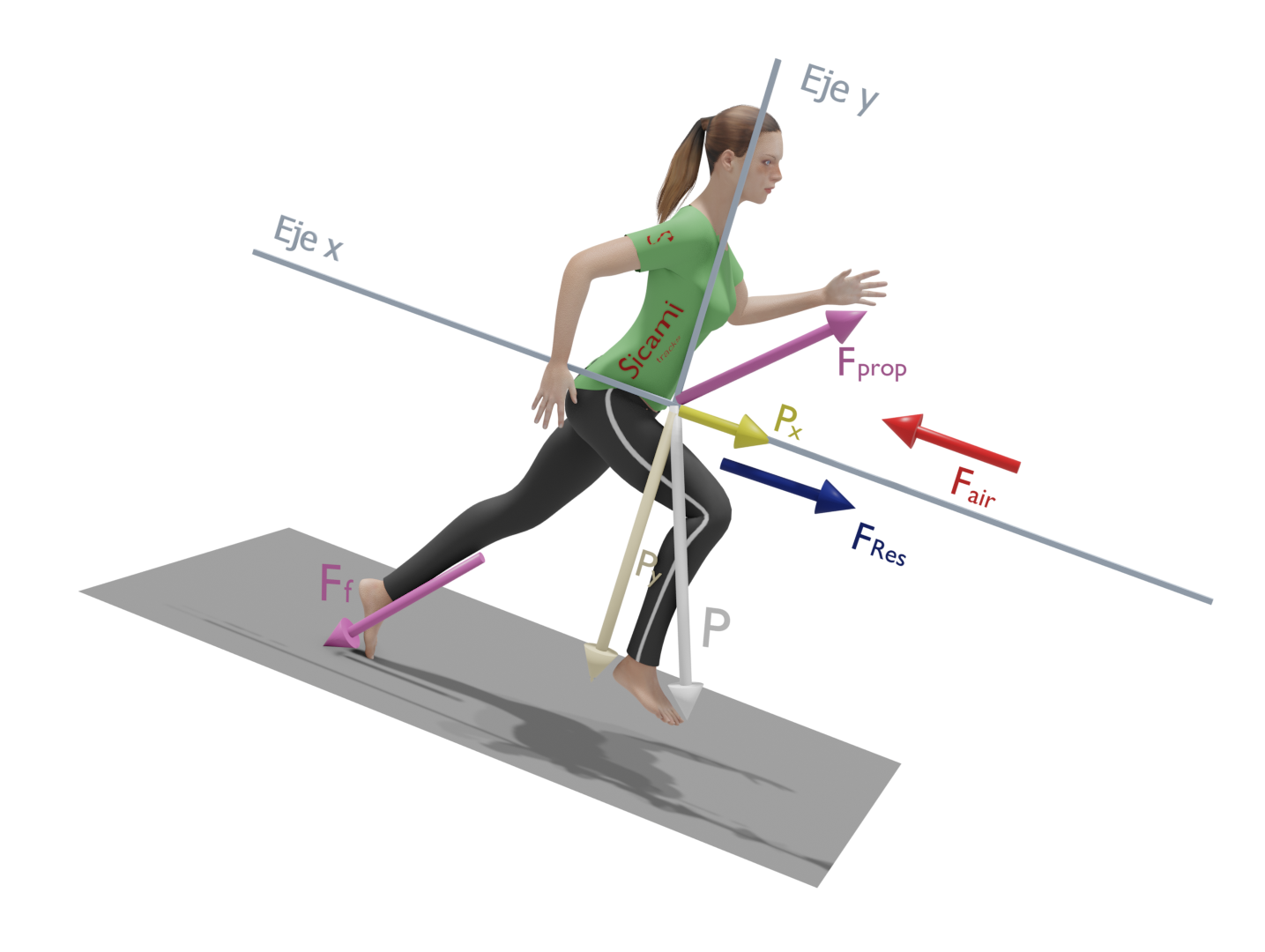
En un esquema simplificado quedaría como muestra la siguiente figura, donde se ha descompuesto la fuerza de propulsión “Fp” en una componente perpendicular al suelo “Fpy” y otra paralela al suelo “Fpx” que debe vencer la resistencia aerodinámica además de proporcionar la aceleración.
La componente “x” de la fuerza gravitatoria tiene la misma dirección y sentido que el desplazamiento, con lo que el esfuerzo para avanzar será menor en este caso.
Física del ciclismo: Fuerzas. Nociones básicas
Fuerzas sobre el ciclista y la bicicleta. Nociones básicas
Cuando circulamos en bicicleta, diversas fuerzas actúan sobre nosotros. Si nos centramos en el avance, las más significativas para alcanzar y mantener una cierta velocidad, son las siguientes.
• Resistencia del aire o resistencia aerodinámica
• Resistencia a la rodadura (rozamiento de las ruedas sobre el suelo)
• Fuerza de atracción de la gravedad (debida al peso del conjunto bicicleta-ciclista)
• Fuerza de aceleración (solo cuando hay cambio de velocidad, no existe a velocidad constante)
• Fuerzas marginales: Fricción de la cadena, engranajes y cojinetes, pérdidas por flexión cuadro…
Estas serían las cinco fuerzas principales que hay que superar para alcanzar y mantener una cierta velocidad. Las fuerzas marginales no las vamos a considerar en lo que sigue, pero se minimizan con un correcto mantenimiento y engrase. El estado final del movimiento dependerá de la diferencia que exista entre las fuerzas en el sentido del desplazamiento y las fuerzas en el sentido contrario al desplazamiento.
Fuerzas sobre el ciclista rodando en llano
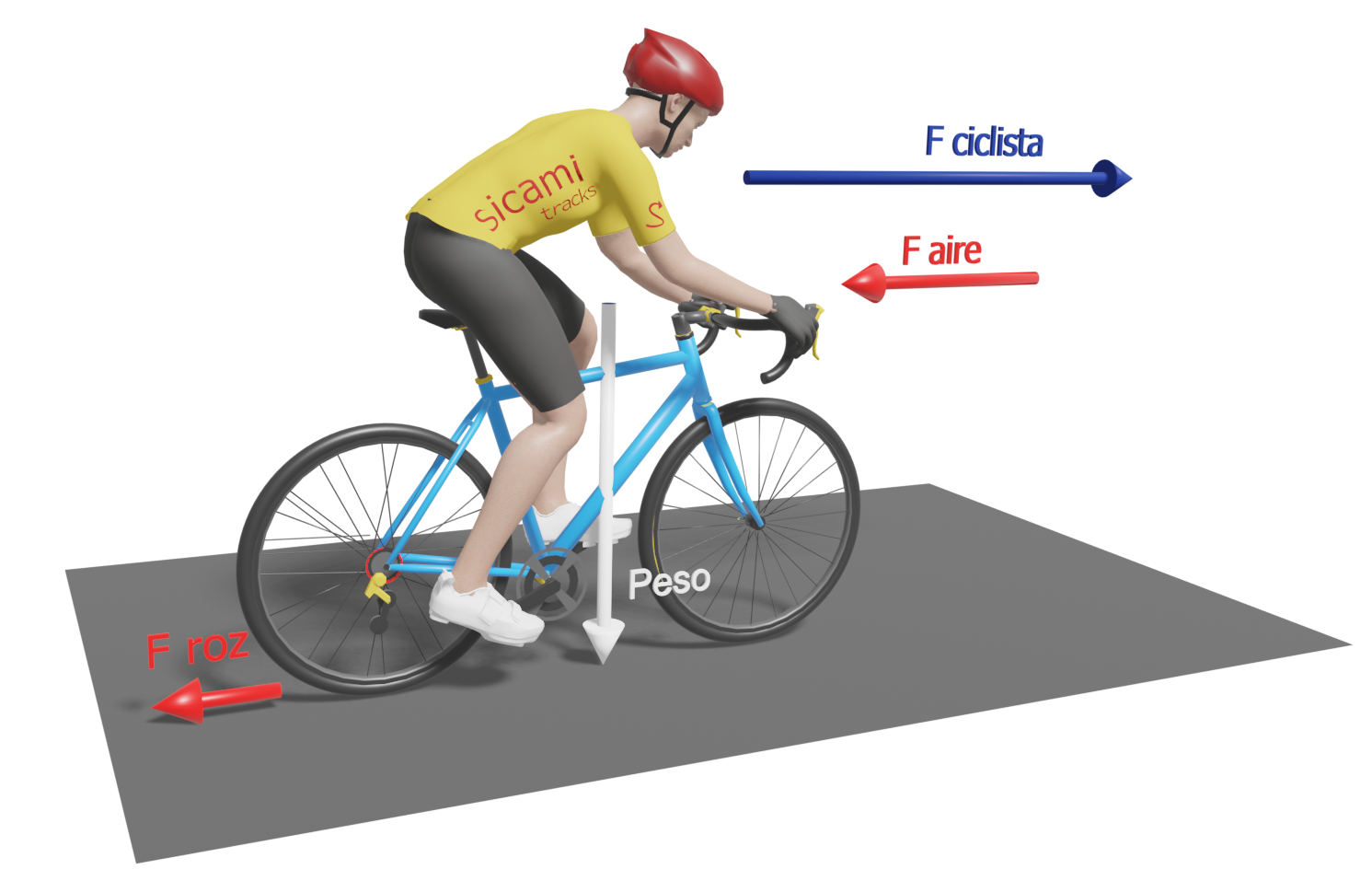 La resistencia a la rodadura resulta del rozamiento de las de ruedas con el terreno y vendrá determinada por las características de los neumáticos y del terreno.
La resistencia a la rodadura resulta del rozamiento de las de ruedas con el terreno y vendrá determinada por las características de los neumáticos y del terreno.##publi##
Fuerzas sobre ciclista ascendiendo
Cuando pedaleamos en ascenso, la resistencia aerodinámica va perdiendo importancia a favor de la fuerza de la gravedad que vendrá determinada por el peso del conjunto ciclista-bicicleta.
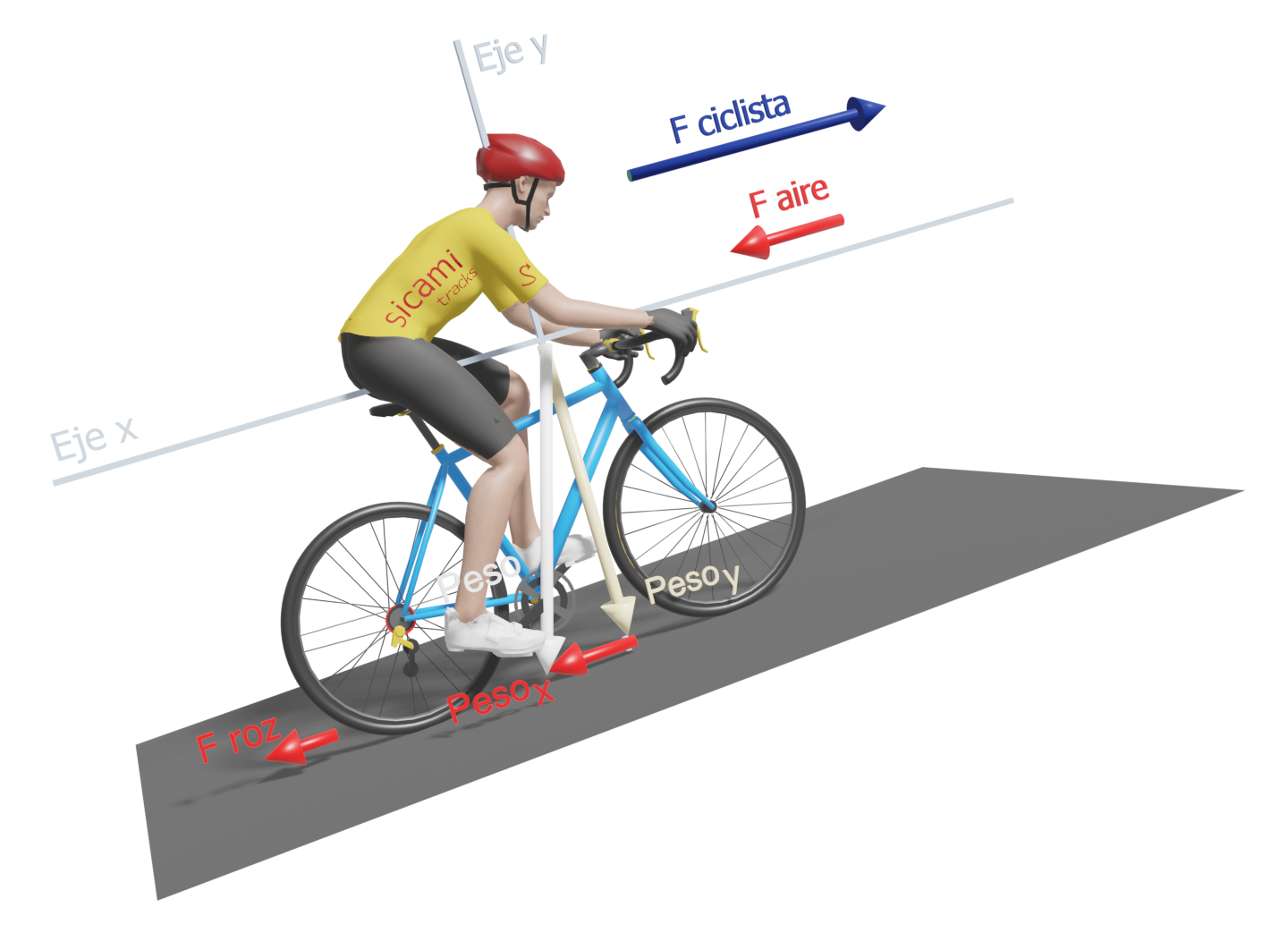
Pero no todo nuestro peso se opondrá al avance. Para verlo con mayor claridad, podemos establecer un sistema de coordenadas que tenga el eje “x” paralelo al suelo y el eje “y” perpendicular. El peso total apuntará hacia el centro de la tierra, pero podemos descomponerlo en dos componentes según cada uno de los ejes de coordenadas establecidos. Así obtendremos una componente sobre el eje “y”, “Peso y” (perpendicular al suelo) y otra sobre el eje “x”, “Peso x” (paralelo al suelo). Esta última componente paralela al suelo es la parte de nuestro peso que realmente se opone a nuestro movimiento de ascenso.
Fuerzas sobre ciclista descendiendo
En el caso de los descensos, la componente “Peso x” apuntará en la dirección del movimiento con lo que se sumará a la que ejercemos al pedalear facilitando el avance. Cuánto más pronunciada sea la pendiente del descenso, mayor será el valor de “Peso x”. Podremos dejar de pedalear cuando esta fuerza supere el valor de la suma de las fuerzas opuestas al sentido del movimiento.
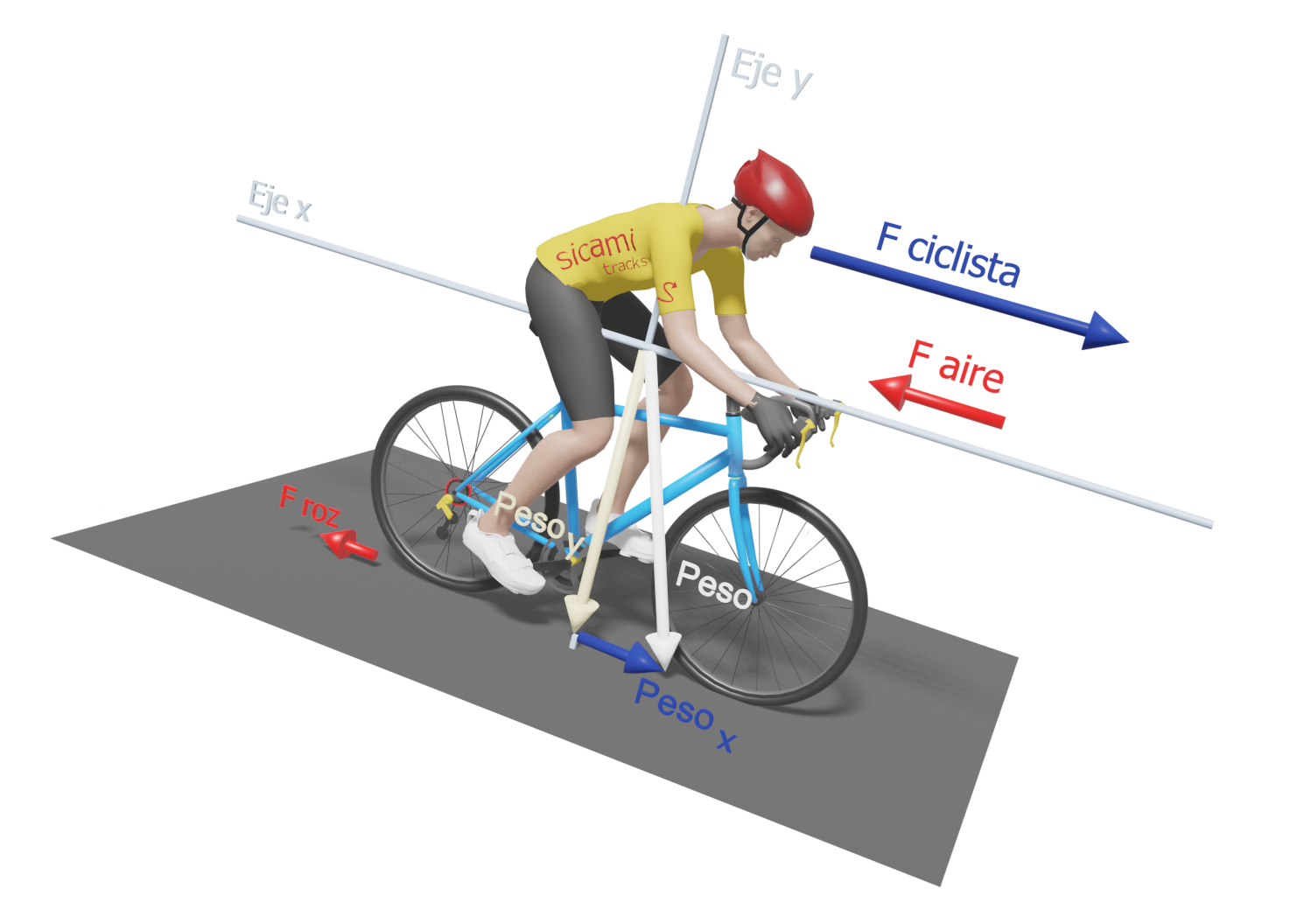
En próximos artículos ampliaremos y profundizaremos en todos estos conceptos.
Artículo recomendado: Aerodinámica fácil para ciclistas y algunos consejos.
Métodos de orientación. Orientarse con un reloj.
Métodos de orientación. Orientarse con reloj.
En primer lugar, es imprescindible que el reloj esté marcando la hora solar o que realicemos el proceso situando mentalmente la aguja horaria en la hora solar que correspondería. La hora oficial dependerá del país y la estación del año y suele variar entre una o dos horas respecto a la hora solar.
Este método no es aplicable en la zona entre los trópicos pues el resultado será variable según la época del año y en determinados momentos la posición del sol estará prácticamente sobre la vertical, no proyectándose sombras. Algo parecido ocurre en verano en las horas centrales del día y cuánto más cerca de los trópicos.
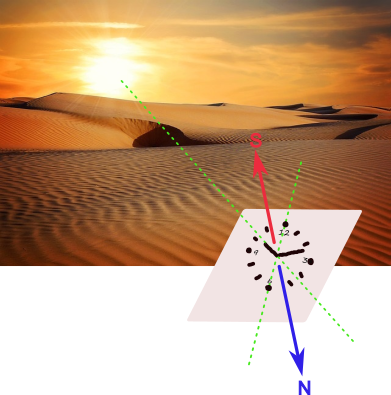
Si estamos en el hemisferio norte
Si nos encontramos en el hemisferio norte, procederemos de la siguiente forma: mantendremos el reloj en posición horizontal, apuntaremos al sol con la aguja horaria. A continuación imaginaremos una línea que pasa por las 12 y las 6. La bisectriz del ángulo que forma la aguja horaria con esa línea 12-6 indicará el sur. Recordar que la bisectriz de un ángulo es la línea que divide ese ángulo en dos partes iguales.
En la dirección opuesta se encontrará el norte. Para hallar el este y el oeste nos posicionaremos mirando hacia el norte, a nuestra derecha quedará el este y a nuestra izquierda el oeste.

Si estamos en el hemisferio sur
Si nos encontramos en el hemisferio sur, deberemos apuntar al sol con el número 12, en lugar de con la aguja horaria y en este caso la bisectriz del ángulo que forma la línea 12-6 con la aguja horaria marcará el norte.En la dirección opuesta se encontrará el sur.

Si no tienes un reloj de agujas
Si no tienes un reloj de agujas pero sabes la hora, siempre puedes dibujarlo en una hoja de papel, en el suelo o utilizando ramitas.
Física. Las leyes de Newton del movimiento.
Las leyes de Newton del movimiento
En 1687 el físico inglés Isaac Newton publicó tres leyes o principios con los que describir el movimiento de los cuerpos en un sistema de referencia inercial, relacionando la fuerza, la velocidad y el movimiento de los cuerpos.
Estas tres leyes son las siguientes
• Primera ley o ley de la inercia.
• Segunda ley o ley fundamental de la dinámica.
• Tercera ley o principio de acción y reacción.
Primera ley de Newton: ley de la inercia
La primera ley o ley de la inercia postula que un cuerpo que esté en reposo o que se mueva en línea recta con una velocidad constante, permanecerá en ese estado, a no ser que se aplique una fuerza externa.

Segunda ley de Newton: ley fundamental de la dinámica
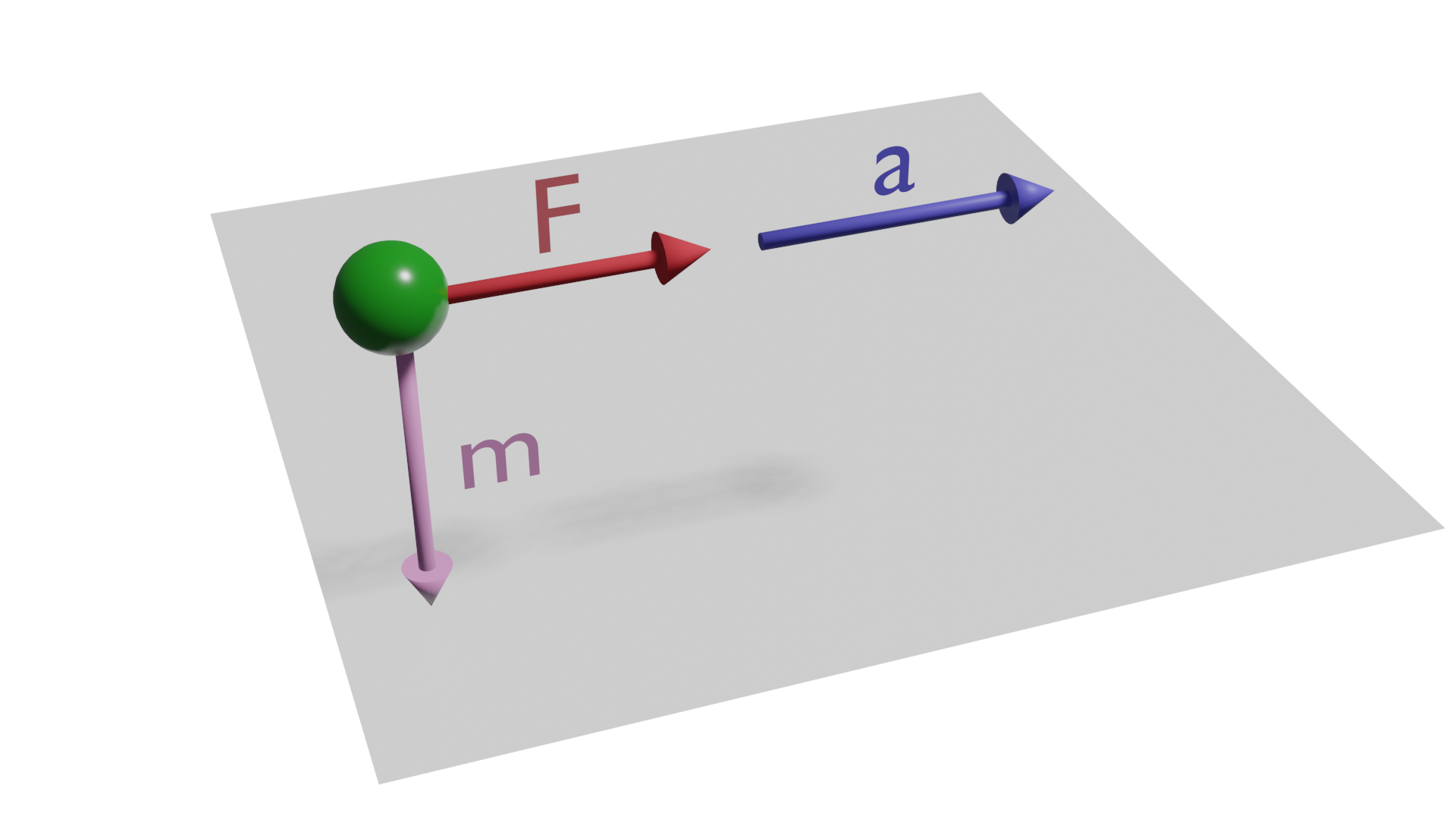
Tercera ley de Newton: principio de acción y reacción
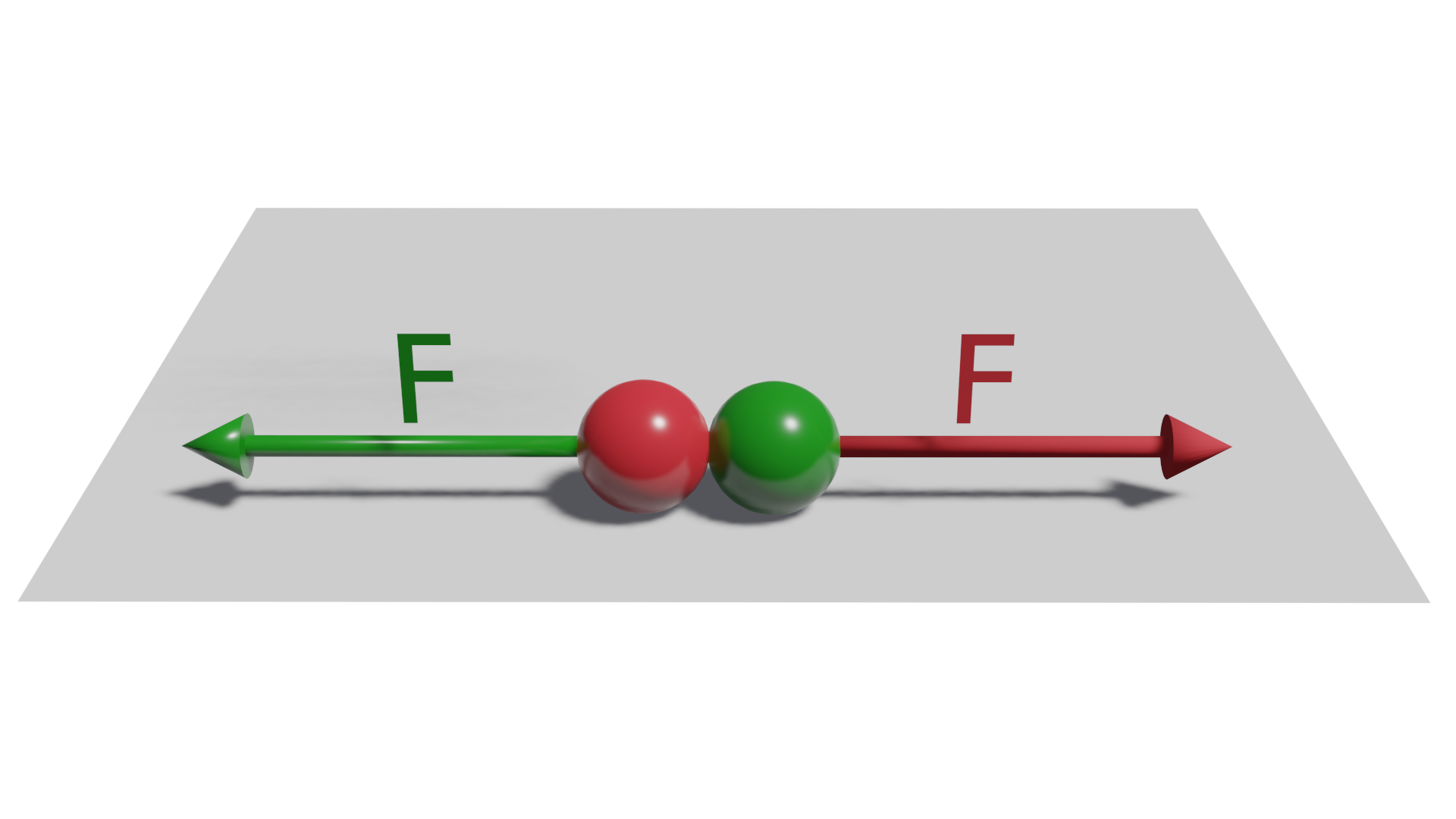
La fuerza del cuerpo A sobre el cuerpo B, F(A-B), que llamaremos fuerza de acción, es igual a la fuerza del cuerpo B sobre el cuerpo A, F(B-A), que llamaremos fuerza de reacción. La fuerza de reacción tendrá la misma dirección e intensidad que la fuerza de acción, pero en sentido contrario.
Con los efectos de esta ley también estamos bastante familiarizados en nuestra vida diaria, por ejemplo, cuando movemos cualquier objeto pesado empujándolo, es decir, aplicando fuerza sobre el objeto para desplazarlo, percibimos una resistencia del objeto que es la fuerza de reacción de este objeto sobre nosotros.
La Ley de Gravitación Universal o Ley de la Gravedad
Ley de gravitación universal o ley de la gravedad
Esta ley describe cómo interactúan y se atraen dos cuerpos con masa, y establece que la intensidad de la fuerza de atracción entre esos dos cuerpos es proporcional al producto de sus masas e inversamente proporcional a la distancia que los separa elevada al cuadrado.
Es decir, la fuerza de atracción será más fuerte cuánto más masa tengan los cuerpos y más cercanos estén, reduciéndose con la distancia.
La fórmula es la siguiente:
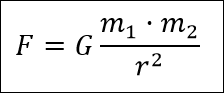
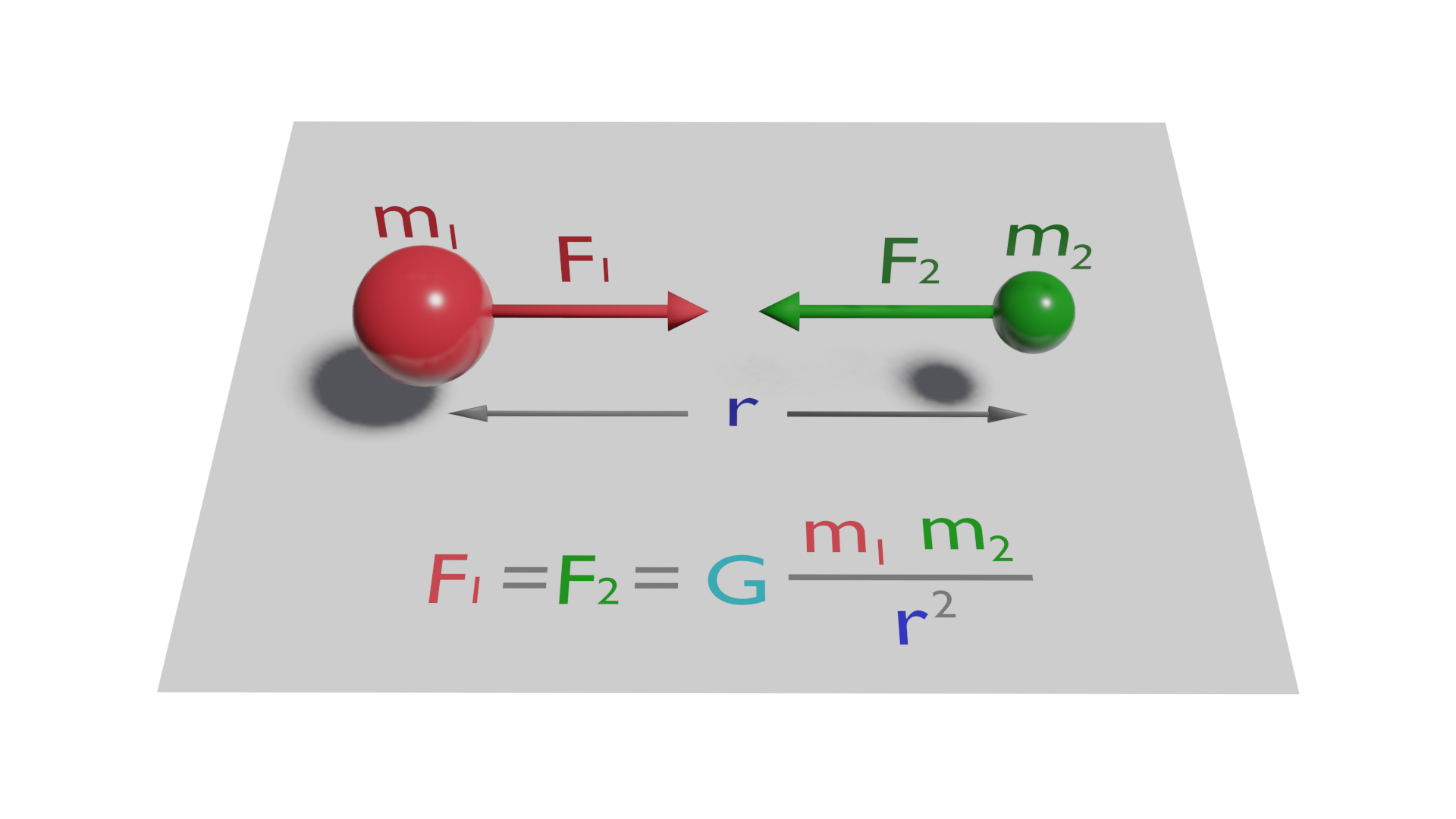
Donde:
F es el valor de la fuerza ejercida entre ambos cuerpos según la línea que los une.
m1 es la masa del cuerpo 1
m2 es la masa del cuerpo 2
r distancia entre los centros de masas de los dos cuerpos
G es una constante, la de gravitación universal, y vale
Calcular la fuerza con la que te atrae la Tierra
Si quieres saber la fuerza con la que la Tierra te atrae necesitas conocer tu masa en kilos, la masa de la Tierra y su radio, que es el la distancia que te separa del centro de masas del planeta.
Si tu peso son 75 kilos:
Masa aproximada de la Tierra: 5,98 × 10^24 kg
Radio medio de la Tierra: 6.37 km = 6.370.000 metros

Fuerzas sobre el pedal. Momento de torsión o torque.
Momento de torsión o torque de la fuerza sobre el pedal
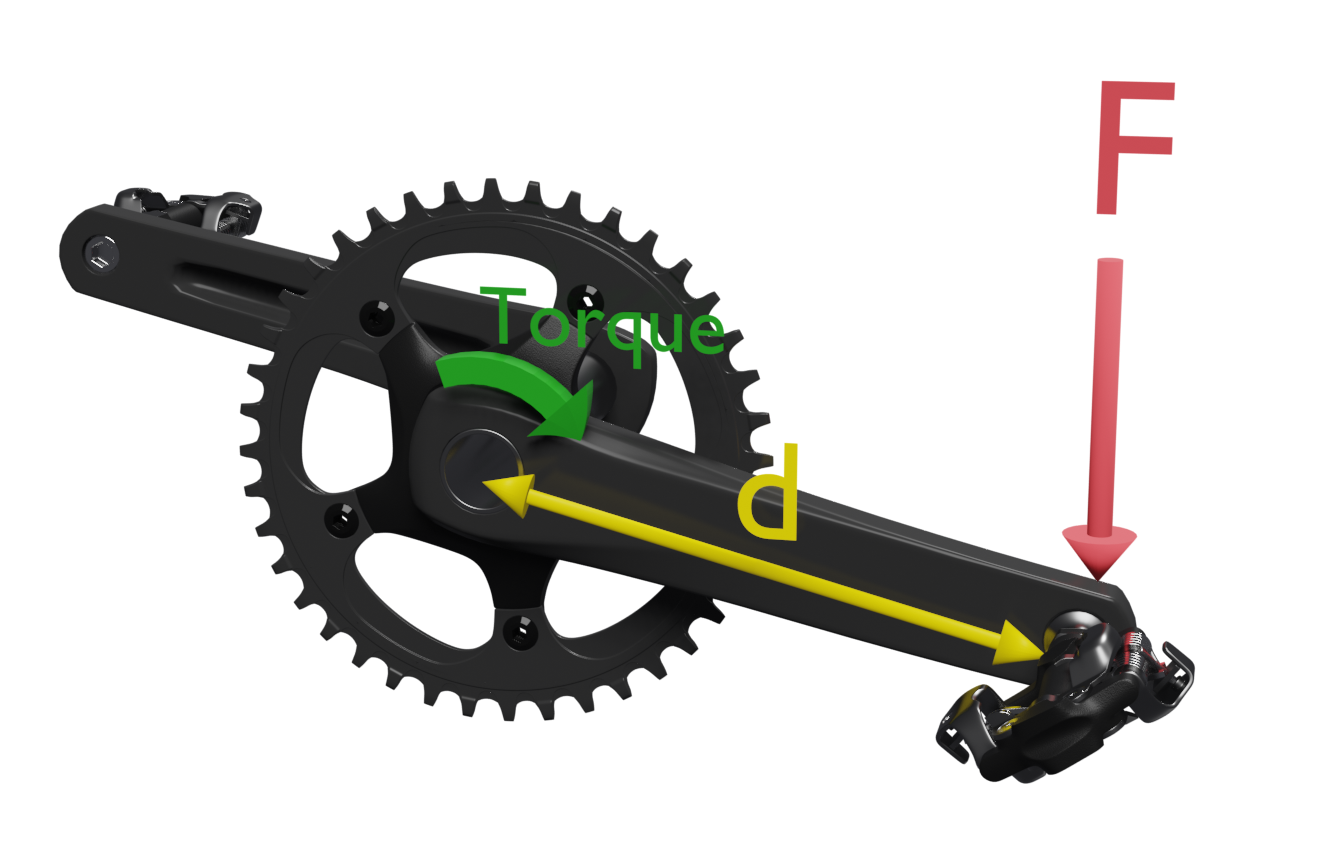
Al pedalear nuestra fuerza se aplica sobre el pedal y se transmite al eje a través de la biela, que actúa a modo de palanca. La aplicación de la fuerza provocará un giro con lo que observaremos un “momento de torsión” o “torque”.
Podemos definir el momento de torsión como la capacidad una fuerza de hacer girar un objeto al aplicarla sobre él.
El valor del momento de torsión de una fuerza se puede calcular como el producto del valor de la fuerza aplicada en un punto, multiplicada por la distancia de ese punto al eje de torsión. Su unidad es el newton por metro.
T = F · d
F = Fuerza sobre el pedal
d = distancia al centro de giro (distancia eje pedal – eje biela)
Componentes tangencial y radial de la fuerza de pedaleo
Pero esto solo sería válido para fuerzas que se apliquen perpendicularmente a la distancia. Cómo la fuerza puede aplicarse en diferentes ángulos, dependiendo de la posición de empuje, ampliaremos la fórmula como sigue:
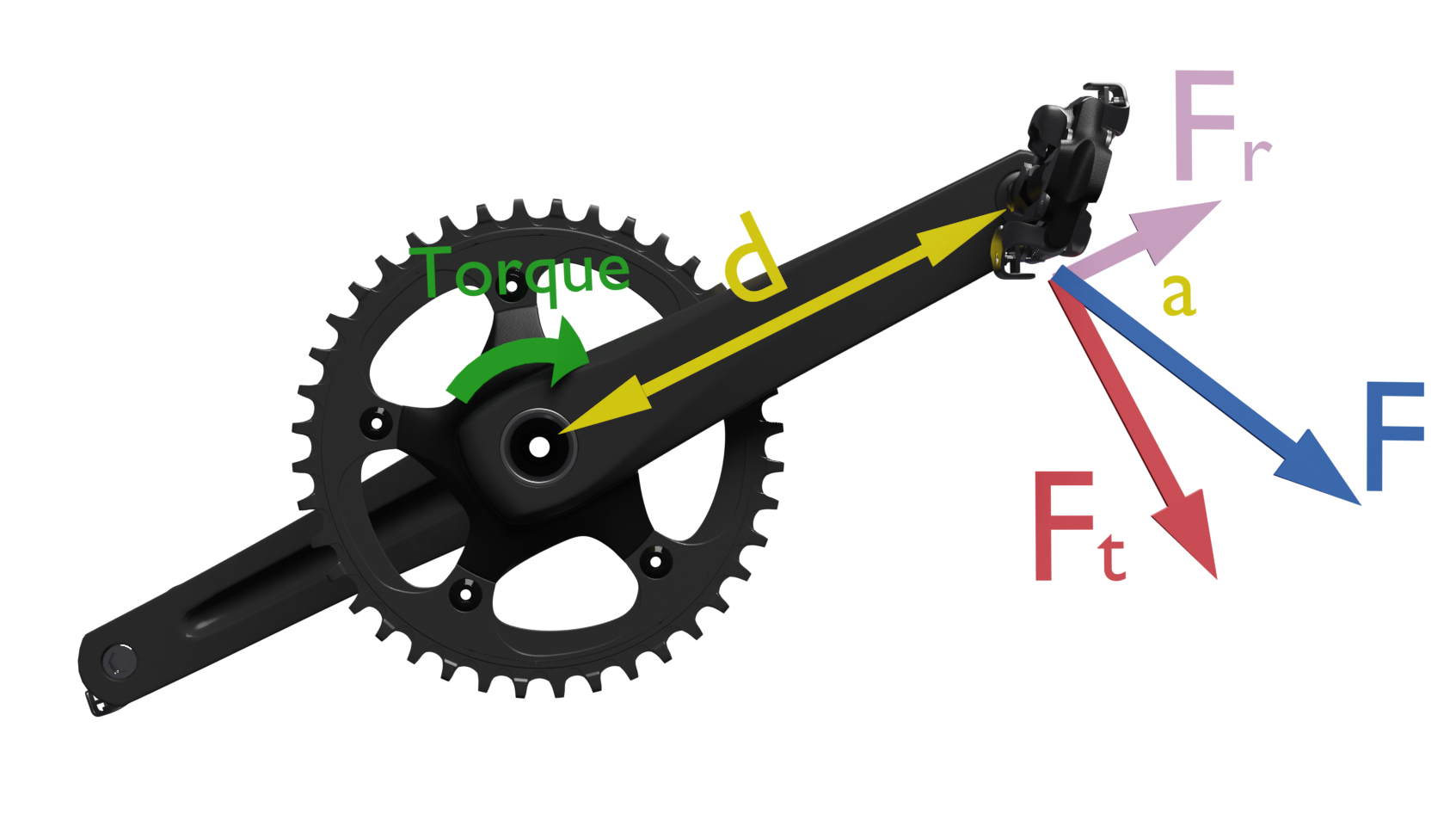
T = F · d · sen (a)
Donde a es el ángulo de aplicación de la fuerza respecto a la línea que une el punto de aplicación y el centro de giro. Siempre se tomará el ángulo cuyo valor sea menor de 90º. Esto es equivalente a descomponer la fuerza ejercida sobre el pedal en dos componentes:
• una componente tangencial Ft, que es tangente a la circunferencia que dibuja el pedal Ft = F sen (a)
• una componente radial, Fr en la dirección de la biela. Fr = F cos (a)
La componente tangencial siempre será perpendicular a la biela y es la que produce momento de torsión útil. La componente radial Fr solo comprimirá o estirará la biela.
Eficacia y eficiencia del pedaleo
La fuerza “útil” dependerá por tanto del ángulo de aplicación de la fuerza sobre el pedal y este a su vez depende fundamentalmente de la posición de las bielas.
Suponiendo que pedaleamos empujando hacia abajo verticalmente, si la biela se encuentra también en posición vertical a las “12-6”, la componente Ft perpendicular a la línea de la distancia será nula y la fuerza aplicada no provocará ningún giro.

Matemáticamente: T = F · sen (0) = F · 0 = 0

Matemáticamente: T = F · sen (90) = F · 1 = F
Conceptos de navegación. Curso y rumbo
Trataremos en este artículo algunos conceptos de navegación y veremos las diferencias entre curso y rumbo
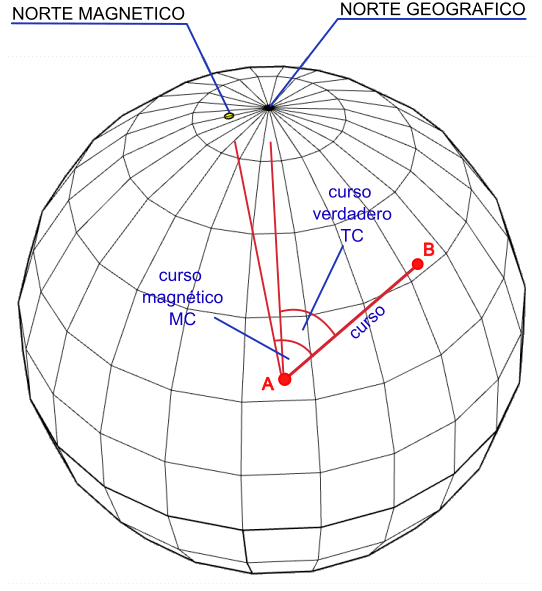
Curso, curso verdadero, curso magnético y curso deseado
Llamaremos curso (course) a la trayectoria a seguir. Es el recorrido planificado o deseado entre dos puntos A y B, es decir, la línea recta que une ambos puntos.
El curso verdadero (TC: True Course) sería el ángulo en grados comprendido entre el norte verdadero o geográfico y el curso. Se mide desde el norte geográfico (o magnético) siguiendo el sentido de las agujas del reloj.
Como los meridianos de un mapa apuntan todos hacia el norte verdadero, se podrán utilizar como referencias de 0 grados para medir los ángulos respecto al norte geográfico.
Ya que el norte geográfico y el polo norte magnético no coinciden (ver el artículo “Declinación magnética” en la sección “Información adicional, curiosidades y glosario de términos” de este sitio), definiremos también el curso magnético (MC: magnetic course) como el ángulo en grados comprendido entre el norte magnético y el curso. Se mide desde el norte magnético y también en sentido horario.
En este caso no se podrán utilizar los meridianos como referencias de 0 grados, así que en su lugar utilizaremos la brújula.
En algunos entornos se denomina indistintamente Curso Deseado (DTK: Desired Track) al curso verdadero y al curso magnético, según el norte utilizado como referencia (geográfico o magnético).
Rumbo, rumbo verdadero, rumbo magnético, deriva y ángulo de corrección de deriva
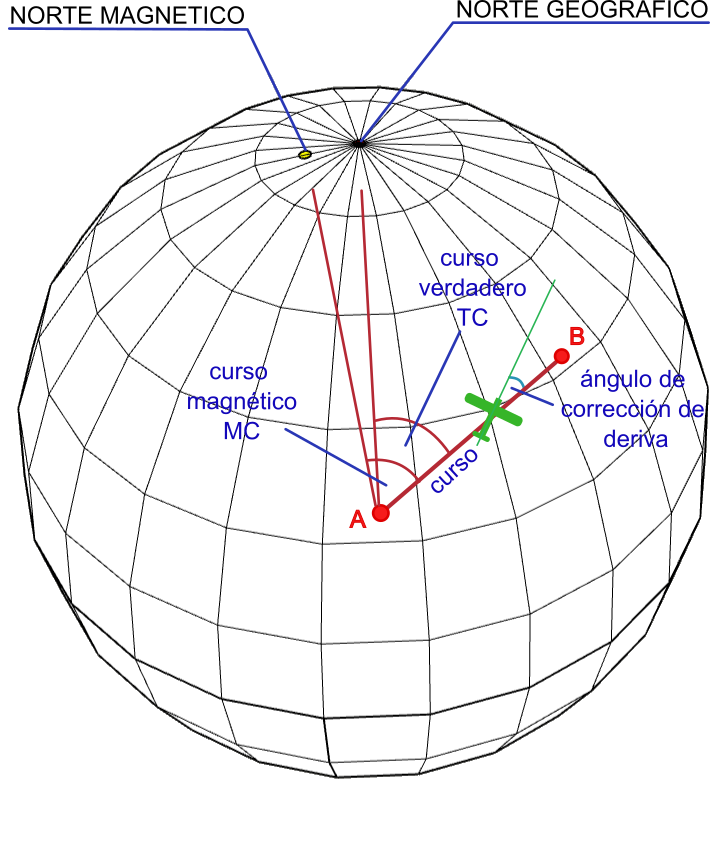
Llamaremos rumbo (Heading) al ángulo formado por el norte (geográfico o magnético) y el eje longitudinal de la aeronave (en el caso de un avión sería hacia donde apunta su nariz). Se llamará rumbo verdadero (TH: True Heading) si el ángulo se toma con respecto al norte geográfico y rumbo magnético (MH: Magnetic Heading) si se toma con respecto al norte magnético.
El rumbo no coincide necesariamente con el curso, ya que la aeronave o buque puede cambiar su orientación para contrarrestar un viento cruzado o corrientes de agua. En el caso de los aviones es habitual que, para mantener el curso constante, la aeronave gire ligeramente la nariz hacia el viento.
##publi##
Al ángulo que se forma entre el curso deseado y el rumbo de la aeronave se le llamará ángulo de corrección de deriva (WCA: Wind Correction Angle) ya que, por definición, la deriva es el desvío de una nave respecto del rumbo establecido, por efecto del viento, del mar o de la corriente.
Básicamente es la diferencia entre hacia donde apunta la nave y hacia donde se está moviendo realmente. Este ángulo lo calcula habitualmente el computador de vuelo. Si el viento viene de la izquierda el ángulo de corrección será negativo, mientras que si viene de la derecha será positivo.
Radios, bujes, llantas, frenos y pares de fuerzas
Radios en ruedas con frenos de disco y frenos de llanta
Existe una diferencia visual inmediata entre las ruedas de bicicleta de carretera que usan freno de disco y las que usan freno de llanta y no está solamente en las zapatas o en los discos, ¿sabrías diferenciar cuál de estos pares de ruedas (igual marca y modelo) corresponde a freno de disco y cual a freno de llanta?


La diferencia es evidente y está en la distribución de los radios de la rueda delantera.
Tradicionalmente los radios de la rueda trasera han sido colocados con un cruzado diferente al de la rueda delantera. En muchos casos los radios de las ruedas delanteras tenían una disposición exactamente “radial”, es decir iban desde el centro de la rueda (el buje) hacia el exterior y llegaban perpendicularmente a la llanta.
Esfuerzos mecánicos sobre las ruedas
El motivo de esto es que los esfuerzos mecánicos a los que está sometida la rueda trasera y la delantera son diferentes, especialmente los esfuerzos de la transmisión. Concretamente la rueda trasera debe transmitir al suelo el par de giro (momento) de la fuerza de la cadena sobre los piñones que a su vez se transmite al buje y desde el buje a la llanta y neumático a través de los radios. De modo que los radios son los “pilares” que transmiten el giro desde el eje de la rueda hasta el suelo.
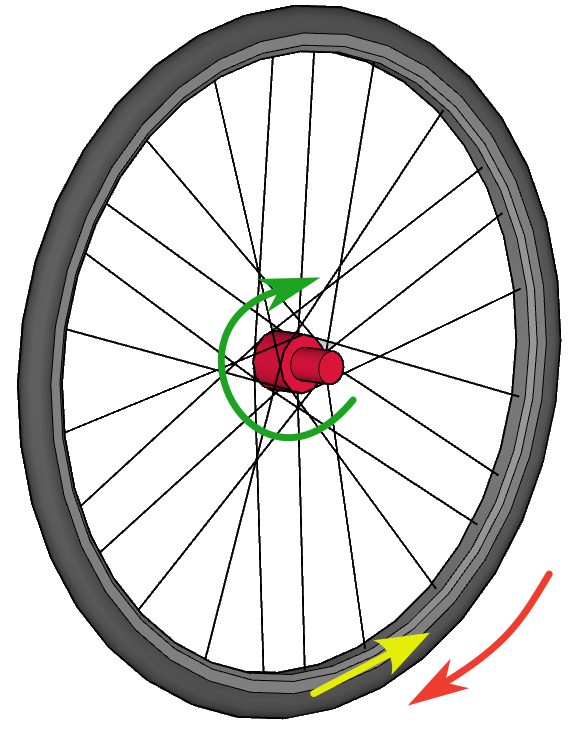
Como el terreno opone resistencia al avance y rotación de la rueda, se generan esfuerzos mecánicos sobre los radios.
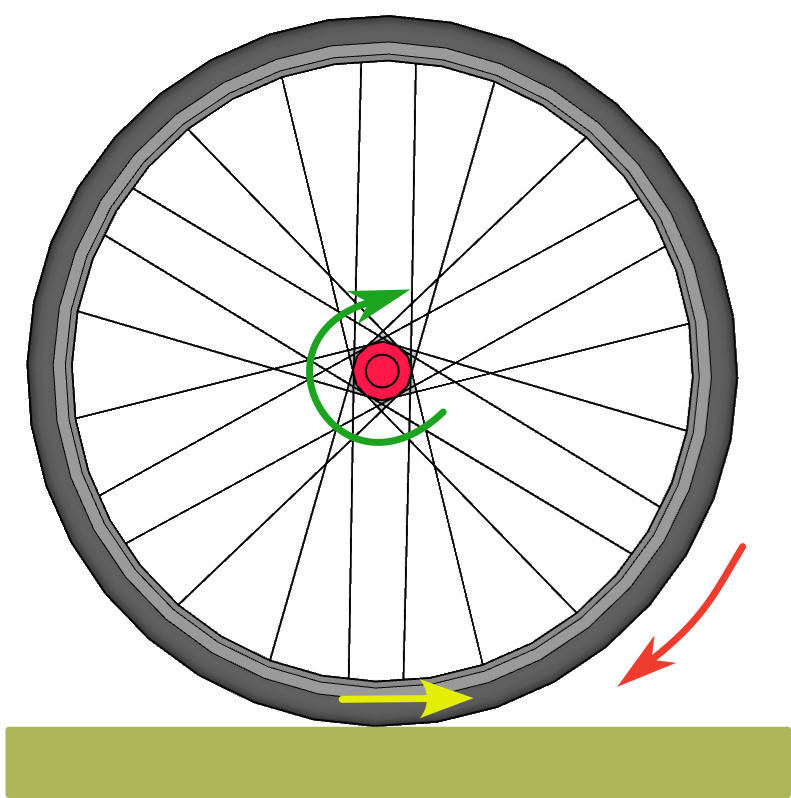
Esfuerzos mecánicos sobre los radios de las ruedas
Los principales esfuerzos a los que se ve sometido un radio serán de compresión-tracción y de flexión pero ¿cómo afectan estos al comportamiento mecánico de los radios?. Los esfuerzos de compresión/tracción actúan en la misma dirección que el eje principal del radio y tenderán a acortarlo (compresión) o alargarlo (tracción). Los esfuerzos de flexión son resultado de fuerzas que actúan perpendicularmente al eje principal y tenderán a doblarlo, por lo que son los que tendrán mayor efecto en que el radio se curve. Debemos considerar que los extremos no sean libres pues en este caso producirán movimientos de rotación y/o traslación. Podemos imaginar que el radio está “momentaneamente” fijado en el punto de contacto con el suelo e imaginarlo como una varilla fijada en ese extremo. El eje-buje de la rueda está aplicando una fuerza sobre ese radio en sentido contrario.
Si pensamos en cuánta fuerza es necesaria para deformar una varilla de cualquier metal, seguramente concluiremos que casi siempre será más fácil romper un lápiz sujetándolo por los extremos y doblándolo que apoyándolo sobre la mesa y presionandolo en uno de los extremos.
Veamos se ven afectados los radios por estas fuerzas según sea su disposición.
Un radio que en el punto de contacto sea perpendicular al suelo, se verá sometido a fuerzas de sentido opuesto en cada uno de sus extremos que provocarán esfuerzos casi exclusivamente de flexión, que son aquellos que tienen mayor efecto en que el radio se curve. En el caso de un radio “cruzado”, en el momento de contacto con el suelo la fuerza que aplica el buje tiene una componente de flexión y otra axial de compresión con lo que parte de esa fuerza total será absorbida por el material. Las fuerzas de compresión tienen un efecto de arqueo sobre una varilla mucho menos relevantes.
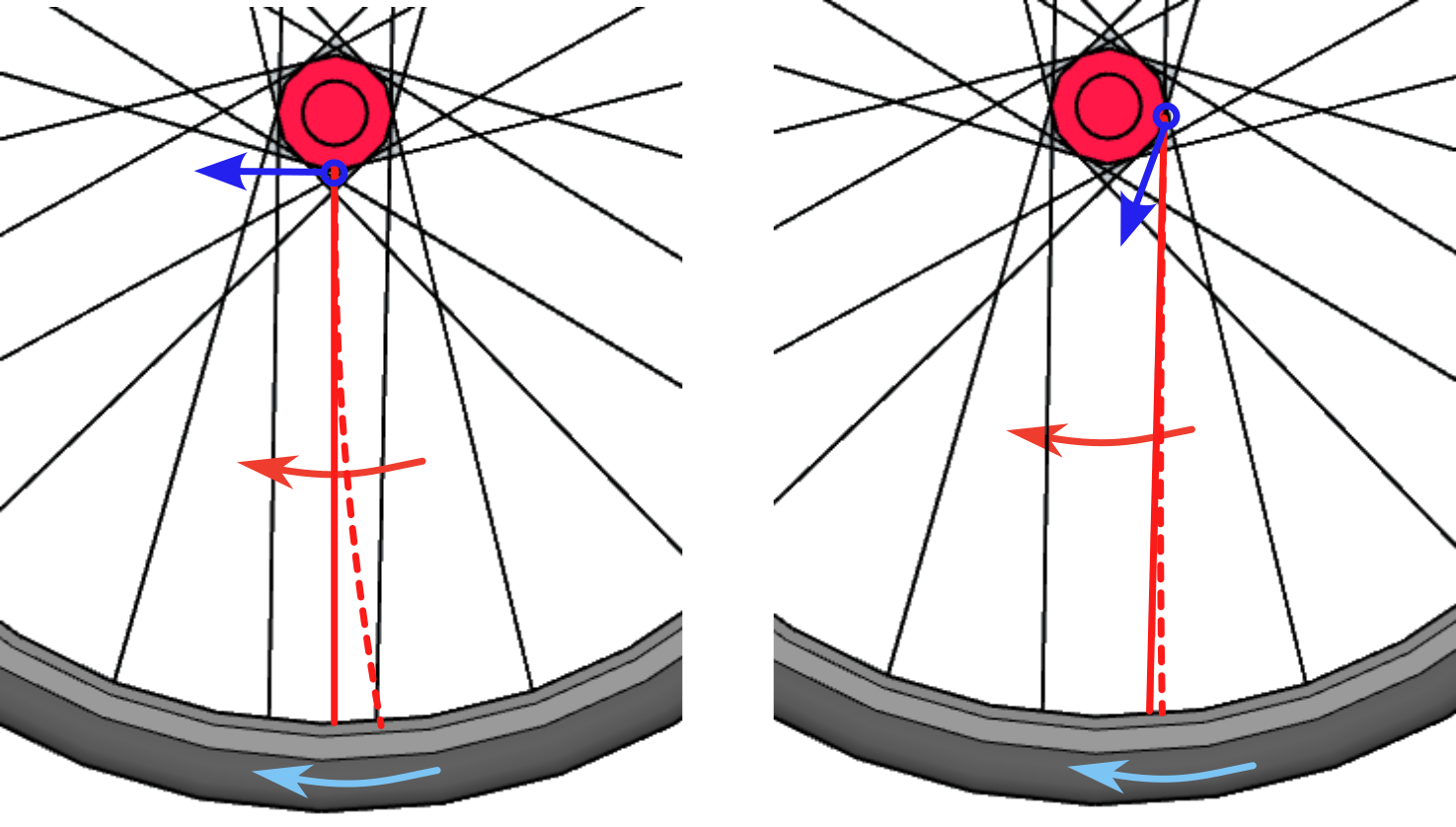
Otra de las fuerzas que actúan sobre estos mismos planos de una rueda son las fuerzas de frenada y no olvidemos que la frenada efectiva se produce en el punto de contacto del neumático de la rueda con el suelo. En el caso de un freno de llanta la fuerza aplicada para detener la rueda se aplica sobre la llanta y ésta la transmite al neumático, situado muy cerca, por lo que es la llanta la que soporta casi todos los esfuerzos con muy poca repercusión sobre los radios. Sin embargo, en el caso de los frenos de disco la fuerza de frenada se aplica sobre un disco solidario con el buje, con lo que esta fuerza debe ser transmitida a la llanta y al neumático, siendo los radios esos elementos de transmisión de fuerzas. Este es uno de los motivos de que actualmente las ruedas delanteras de las bicicletas de carretera que montan frenos de disco hayan abandonado la disposición radial y adoptado también la disposición de radios cruzados tradicional de las ruedas traseras.
¿Podría ser este el verdadero motivo de la rotura de radios de la rueda con frenos de disco de Wilco Kelderman en el Giro de Italia de 2022, cuando perdió casi 11 minutos en los descensos?. Algunos lo achacaron al "calentón" de los radios por el freno de disco, aunque parece dificil que tanta cantidad de calor pueda transmitirse desde el disco al radio y que esta llegue a destruirlo. Quizás aquellos radios simplemente no soportaron los intensos y repetidos esfuerzos de flexión de las fuertes y largas frenadas del descenso.
Geometría de la bicicleta: Batalla o distancia entre ejes.
Batalla o distancia entre ejes. Influencia en el carácter y comportamiento de la bicicleta.
A la distancia que existe entre los ejes (bujes) de las ruedas, medidos desde su centro se le denomina también "batalla", en inglés wheelbase y es un elemento muy determinante en el caracter de la bicicleta. Cuanto más corta sea la batalla más reactiva, ratonera en curvas y nerviosa será la bicicleta, también más rígida y por tanto menos confortable, mientras que batallas más largas harán a la bicicleta más estable y confortable, sobre todo en terrenos rectos y a mayores velocidades, pero también más lenta en sus reacciones. La distancia entre ejes influye directamente en el radio máximo para virar que tiene la bicicleta
La distancia entre ejes obviamente depende del resto de elementos de la bicicleta y de su geometría general, aunque algunos de los elementos más determinantes son la talla, el ángulo de la dirección y el avance de la horquilla o flecha. En la siguiente imagen se muestra como una horquilla con avance (imagen superior) aumentará la distancia entre los ejes mientras que una horquilla recta la disminuirá.
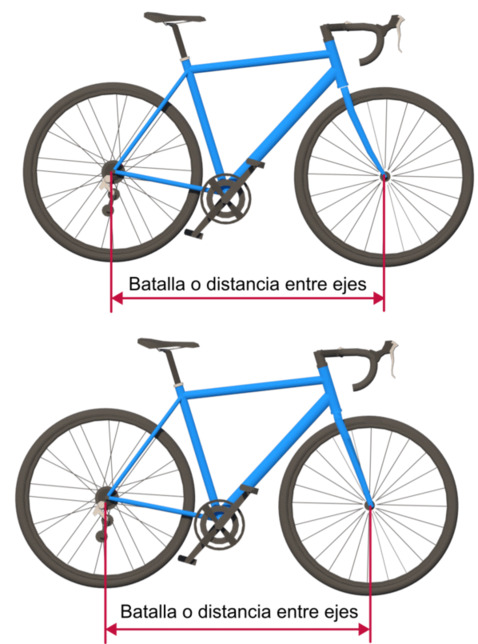
La distancia entre ejes de las bicicletas de carretera es notablemente más corta que en las bicicletas de montaña. En estas últimas, la batalla es más larga para así poder rodar mejor por terrenos más exigentes. Esta diferencia de longitud puede ser de 100 mm. o más.
Hay muchos más elementos que determinan el comportamiento de una bicicleta y su influencia no es individual, ya depende del resto de componentes incluido el ciclista y en cualquier caso, sería el resultado de la combinación, no necesariamente la suma, de todos ellos. Tengamos en cuenta que la bicicleta, al contrario que un automóvil o motocicleta, tiene una masa total mucho más reducida pero y esto es muy importante, la distribución de estas masas es muy diferente. El elemento de mayor masa en el conjunto bicicleta-ciclista es este último que, junto a su posición, hará que el centro de masas del conjunto esté a mayor altura relativa que en automóviles o motocicletas.
##publi##
No olvidemos que la distancia vertical del centro de masas del vehículo determina el momento de las fuerzas que se ejercen sobre el vehículo, incluido su "momento de vuelco". Estos momentos son tanto mayores cuando mayor es la distancia del centro de masas al suelo. Esta es una de las razones por la que es recomendable bajar la posición del cuerpo al tomar curvas, porque se ganará estabilidad y seguridad pudiendo trazarse a mayor velocidad.
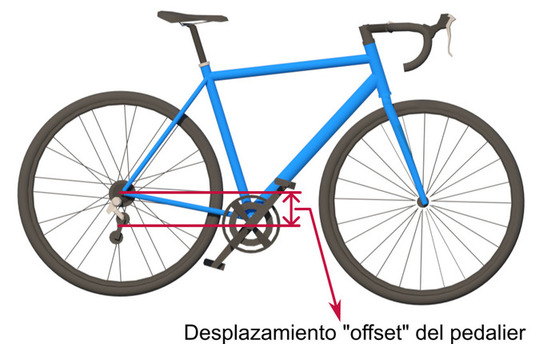
En cuanto a la geometría de la bicicleta, el "desplazamiento del pedalier", también conocido como "offset del pedalier" es el que determina en mayor medida la posición del centro de gravedad. Se trata de la distancia vertical entre la horizontal del pedalier y la horizontal de los bujes de las ruedas. Pero hablaremos de este parámetro en otro artículo.
Geometría de la bicicleta: Altura y longitud del cuadro. Stack y reach
Geometría clásica de la bicicleta
La forma de la bicicleta ha evolucionado notablemente a lo largo del tiempo. Aunque la geometría más habitual durante las últimas décadas ha sido la formada por dos triángulos adyacentes unidos por el tubo del sillín.

Durante muchos años una característica común a todos los cuadros fue la horizontalidad del tubo que une sillín y manillar. La longitud de ese tubo determinaba en gran medida la talla de la bicicleta.

Tubo "horizontal" inclinado. Sloping
En la actualidad, debido a la incorporación de nuevos materiales y procedimientos de fabricación, la tendencia es que ese tubo, que durante años permaneció horizontal, ahora aparezca inclinado (sloping). Con esta modificación se acorta el tubo del sillín, lo cual aumenta la rigidez (menor flexibilidad) del cuadro al hacer más pequeño el triángulo posterior y reduce algo los materiales empleados y, por tanto, el peso del conjunto. Además, permite reducir el número de tallas ofrecidas por el fabricante ya que la tija del sillín permitirá mayor margen de ajuste. Por otro lado, los cuadros más compactos y resistentes son más reactivos y facilitan la manejabilidad de la bicicleta, aunque se penalice algo la estabilidad en bajadas y en curvas a alta velocidad.

El gran inconveniente de esta modificación es que dificulta en gran medida la elección de la talla de la bicicleta y la comparativa entre las dimensiones de diferentes modelos y entre diferentes fabricantes.
Stack y reach. Altura y alcance
Para resolver este problema podemos recurrir a dos medidas que definirán perfectamente la geometría de un cuadro en cuanto a su tamaño, estas son la altura (stack) y la longitud o alcance (reach) y tendrán como punto de referencia el eje del pedalier y la parte superior del tubo de dirección (medido en su eje).
Se definirá la altura o stack de un cuadro como la distancia vertical entre el eje del pedalier y la parte superior del tubo de dirección.
La longitud, alcance o reach será la distancia horizontal entre el eje del pedalier y la parte superior del tubo de dirección.
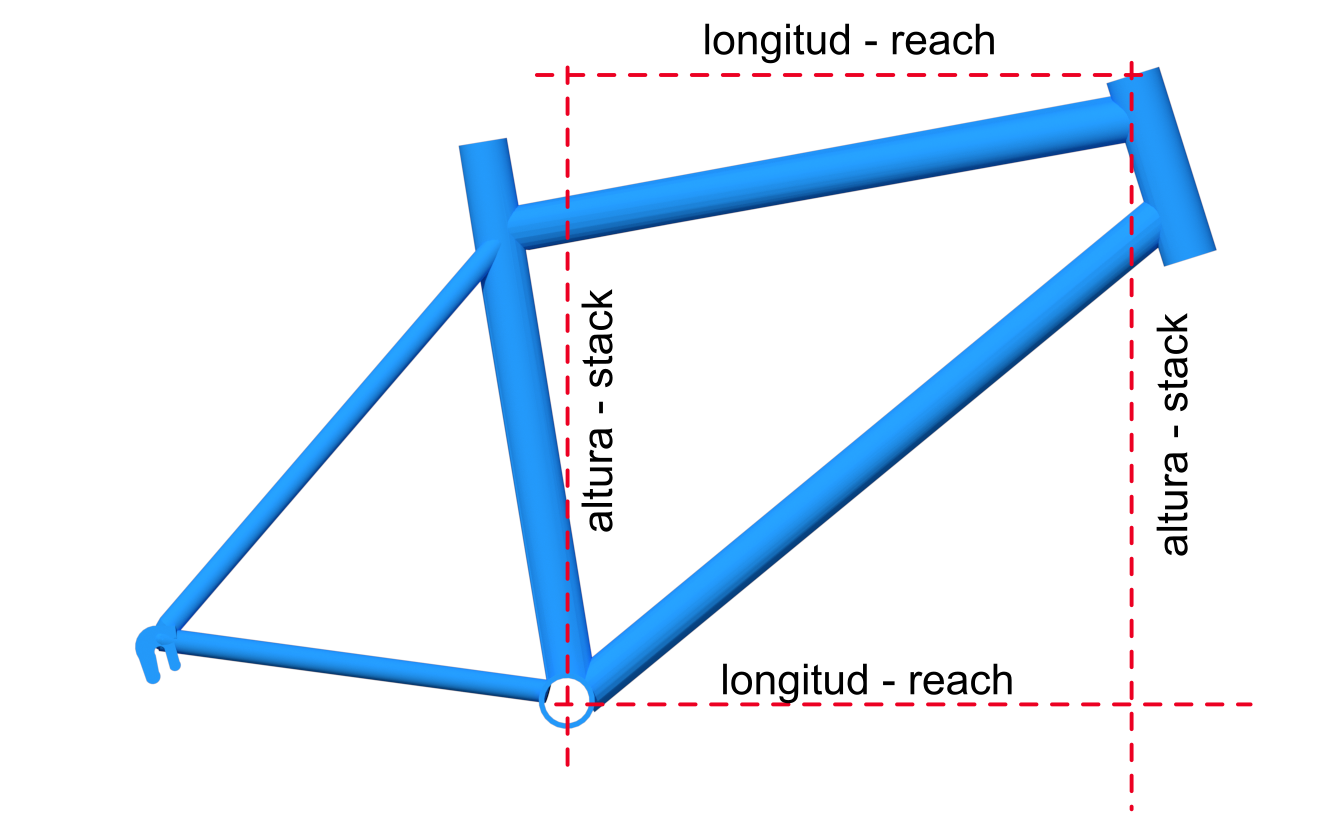
Como no vamos a encontrar ningún elemento exactamente horizontal ni vertical en el cuadro, ambas serán líneas imaginarias por lo que necesitaremos utilizar alguna herramienta, como un nivel de burbuja, para poder determinarlas.
En próximos artículos desarrollaremos el tema de las tallas de la bicicleta y la importancia de su correcta elección.
Nudos básicos, útiles y fáciles de realizar
La cuerda
Si hay un elemento que verdaderamente puede resultar útil cuando nos movemos en entornos naturales, ese elemento es, sin duda, la cuerda. A lo largo de nuestra dilatada experiencia realizando deportes en entornos naturales nos hemos encontrado en múltiples ocasiones con circunstancias en las que fue necesario utilizar cuerdas para solventar alguna eventualidad. Obviamente en la escalada o la progresión por vías ferratas es un elemento indispensable y su conocimiento y manejo es una cuestión de máxima seguridad. Pero también ha demostrado su utilidad en muchas otras condiciones, especialmente en reparaciones de emergencia o simplemente para asegurar elementos evitando su pérdida.
Siempre podrás encontrar algún lugar para ir bien equipado.

¡Advertencia! algunas actividades deportivas requieren del conocimiento y dominio de la técnica específica, por favor no asumas riesgos innecesarios y asesórate con un profesional experto conocedor de los riesgos y técnicas de la actividad

Los nudos
Pero para que una cuerda sea realmente útil es necesario modificar su forma convenientemente, para esto utilizaremos nudos. Por definición un nudo (del latín nodus) es un lazo que se estrecha y cierra de modo que con dificultad se pueda soltar por sí solo, y que cuanto más se tira de cualquiera de los dos cabos, más se aprieta.
Las principales características que debe cumplir un nudo son: que sea fácil de elaborar, que sea fácil de deshacer tras su uso con carga, que sea resistente y que sirva para el propósito que vayamos a darle.
Partes de la cuerda y del nudo
En primer lugar, algunas definiciones...
Cabo: un cabo es otra forma de llamar a una cuerda.
Chicote: es el extremo de la cuerda, la punta.
Firme: es el resto de la cuerda respecto a uno de sus chicotes.
Seno: es un bucle, lazo o pliegue de la cuerda. También se produce al cruzar el chicote sobre el firme.

Cordino: Llamaremos así a las cuerdas de menor calibre, 4-8 mm.
Algunos nudos comunes
Nudo de ocho
Es el nudo más usado en escalada para unir el arnés a la cuerda. Se trata de un nudo muy seguro y resistente, de fácil ejecución y fácil de desenlazar cuando ha estado sometido a carga. Existen dos modos de construirlo que se utilizarán según el caso. La forma básica se construye como se muestra en la figura:

Nudo de ocho por seno
Se podrá emplear siempre y cuando el elemento de anclaje permita su apertura, como el caso de mosquetones, maillones, etc. ya que partiremos de un lazo cerrado. Para realizarlo haremos un nudo simple pero dando una vuelta adicional.
En el primer paso haremos un lazo o seno que pasaremos por encima y alrededor del firme dándo la vuelta por detrás de éste, de forma que se creará otro bucle, en este caso formado por una doble cuerda. Posteriormente pasamos el extremo del lazo por el interior del seno formado. Ya solo queda tensar y "peinar" de modo que quede como muestra la última figura.

Nudo de ocho por chicote
Emplearemos este método cuando sea necesario pasar el chicote por el elemento de anclaje cuando éste es cerrado, como en el caso del arnés, anillas, etc. Para su construcción partimos del nudo de ocho básico y pasaremos el chicote a través de la argolla, arnés... A continuación iremos siguiendo con el chicote el trazado del nudo base en sentido inverso.

Nudo as de guía
Otro de los nudos más utilizados en escalada y rescate, también para elevar cargas. Es un nudo que no se desliza y que es fácil de realizar y de deshacer. Este nudo solamente debe usarse bajo carga pues se queda abierto en cuanto desaparece la tensión.
Se comienza realizando un lazo simple, en la figura inferior el extremo libre lo hemos pasado por encima del firme. A continuación pasar el chicote por el lazo desde abajo hacia arriba y rodear el firme por detrás. Volver a pasar el chicote por el lazo, pero esta vez desde arriba hacia abajo. Tensar. Para aumentar la seguridad del nudo evitando que se dehaga fácilmente al estar sin tensión es recomendable rematar el extremo sobrante con algún nudo sencillo adicional.

Lo habitual es que el punto de anclaje sea cerrado, como en el caso de una argolla o que la parte abierta sea inaccesible, como en un árbol, poste alto, etc... por lo que es conveniente practicar la ejecución por chicote tal como se muestra en las siguientes figuras.

Nudo de ballestrinque
Suele utilizarse para asegurar la cuerda en un poste, barra o a otro cabo, por lo que es muy utilizado para los soportes de las tiendas de campaña. Es un nudo que tenderá a aflojarse si se somete a esfuerzos desde distintas direcciones.
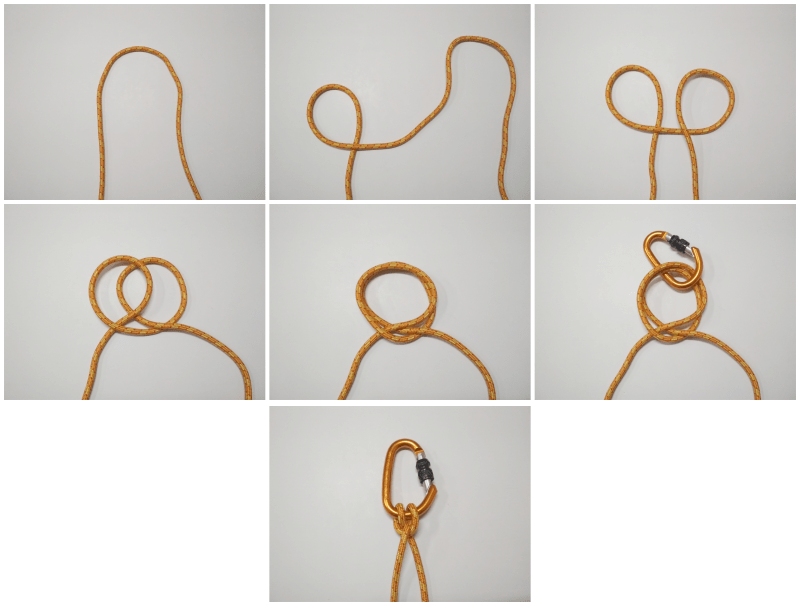
Igual que en casos anteriores si el punto de anclaje es cerrado o no tiene accesibles los extremos será necesario aplicar el método de construcción por chicote.

Nudo de pescador doble
Lo utilizaremos para unir dos cuerdas entre sí o para cerrar una cuerda o cordino en forma de anillo. Esto último será imprescindible para poder realizar algunos de los nudos que mencionaremos más adelante.

Nudo de alondra
Nudo muy sencillo para anclaje directo sobre anillas o postes. Es habitual realizarlo con un lazo cerrado en anillo.

Aunque también es posible realizarlo con un cabo abierto. Es recomendable asegurar en nudo pasando interiormente el extremo corto sobrante.

Nudo romano
Es un nudo en el que las cuerdas saldrán en sentidos opuestos creando un lazo direccional alineado hacia arriba o hacia abajo respecto a la línea de cuerda principal. Tiene aplicación en izado, polipastos, tensado de cuerdas, estribos, ….

Nudo de ocho en línea
Similar al nudo romano, pero en este caso está basado en un nudo de ocho. Las cuerdas también saldrán en sentidos opuestos creando un lazo direccional alineado hacia arriba o hacia abajo respecto a la línea de cuerda principal. La aplicación también será en izado, polipastos, tensado de cuerdas, estribos, ….

Nudo de Prusik
Es un nudo autoblocante para el que se utiliza un cordino en un lazo cerrado en anillo. Se utiliza sobre otra cuerda principal de mayor diámetro. El nudo desliza con facilidad cuando no está sometido a carga, pero se bloquea en cuanto recibe tensión ya que aprisiona la cuerda principal. Se utiliza como método de autoaseguramiento en rapel, para remontar sobre cuerda, descender equipo… Se construye rodeando la cuerda tal como se muestra en las figuras pasando sucesivamente uno de los extremos por debajo del lazo principal. Es muy importante acomodar bien el nudo a la cuerda antes de utilizarlo. Al ser un nudo simétrico actúa en ambas direcciones.

Nudo de Machard
Es otro nudo autoblocante para el que también se utilizará un cordino en un lazo cerrado en anillo. Se utiliza sobre otra cuerda principal de mayor diámetro. El nudo desliza con facilidad cuando no está sometido a carga, pero se bloquea en cuanto recibe tensión al aprisionar la cuerda principal. Se utiliza como método de autoaseguramiento en rapel, para remontar sobre cuerda, descender equipo… Se construye rodeando la cuerda principal tal como se muestra en las figuras para terminar pasando el extremo inferior por el lazo superior. Es muy importante acomodar bien el nudo a la cuerda antes de utilizarlo. Este nudo, a diferencia del Prusik solo actúa en una dirección.

La diversidad de nudos existente es inmensa y daría para un tratado específico que no es el objetivo de este sitio, te invitamos a que profundices en este apasionante tema.
Glosario de términos

GPS (Global Positioning System) y otros sistemas de posicionamiento global
Los sistemas de posicionamiento global son sistemas que permiten localizar un objeto que esté sobre la Tierra con una alta precisión.
Más información en este enlace Sistemas de Posicionamiento Global
Coordenadas geográficas
Sistema de referencia de coordenadas angulares esféricas para representar localizaciones en la tierra. Se necesitarán al menos tres valores para representar una ubicación: una para la posición horizontal, otra para la posición vertical y una tercera que indique la distancia a la cota cero, que se identifica como la del nivel del mar. Los valores de posición horizontal y vertical se dan habitualmente en grados sexagesimales, ya que se trata de ángulos cuyo centro es el de la Tierra.
Más información en este enlace Coordenadas geográficas
Waypoint (punto de referencia)
Es una posición concreta de un punto de la Tierra definida por unas coordenadas geográficas. Se le identifica por un nombre y habitualmente incorpora un icono o símbolo gráfico y otra información adicional como un comentario, fecha, altitud.
Sistemas de notación: grados sexagesimales y grados decimales
El sistema sexagesimal se utiliza para expresar medidas de tiempo y ángulos utilizando tres grupos de valores: grados, minutos y segundos. Tiene como base el número 60 y es el sistema utilizado tradicionalmente en los mapas en papel.
Tiempo: 1 h 60 min 60s
Ángulos: 1º 60’ 60”
En el caso de las coordenadas geográficas, para la latitud se suele indicar, además, el hemisferio al que pertenecen, norte (N) o sur (S) y para la longitud, si están al este (E) o al oeste (O) (W en inglés).
Por ejemplo: 39°49'51.8"N 3°46'49.2"W
Hemisferio norte: Latitudes entre 0° y 90 °
Hemisferio sur: Latitudes entre 0° y -90°
Al este del meridiano de Greenwich: Longitudes entre 0° y 180°
Al oeste del meridiano de Greenwich: Longitudes entre 0° y -180°
En aplicaciones informáticas suele emplearse el sistema decimal, en el que se transforman los minutos y segundos en un número decimal.
39°49'51.8"N 3°46'49.2"W = 39.831045, -3.780322
Para la conversión manual de grados sexagesimales a grados decimales se realiza la suma de:
Grados + minutos divididos por 60 + segundos divididos por 3600:
Ejemplo:
39°49'51.8"N = 39 + (49/60) + (51.8/3600) = 39.8310
3°46'49.2"W = 3 + (46/60) + (49.2/3600) = 3.7803
Para realizar la conversión existen múltiples aplicaciones y calculadoras en internet
.
Desniveles y pendientes
El desnivel, por definición, es la diferencia de altura entre dos o más puntos. El punto de nivel cero será el punto donde comencemos la ruta, independientemente de la altura de ese punto al nivel del mar.
Más información en este enlace Desniveles y pendientes
Altitud, Altura y Elevación
Es común utiilizar indistintamente los términos altitud y altura para referirnos a una ubicación. A continuación vamos a recordar la definición de estos términos.
Más información en este enlace Altitud, Altura y Elevación
Nociones básicas sobre interpretación de mapas: curvas de nivel
Para la representacion de la distribución de una variable (temperatura, presión atmosférica...) sobre una superficie se utilizan isolíneas. Las isolíneas son líneas que unen puntos con igual valor en la superficie, el valor puede ser aquel que se escoja, temperatura (isotermas), presión (isobaras), precipitación (isoyetas).
Más información en este enlace Nociones básicas sobre interpretación de mapas
Declinación magnética
El campo magnético generado por la Tierra no es inmutable, por el contrario, varía constantemente tanto en su posición como en su intensidad y además, periódicamente (en ciclos de miles de años) se invierte. En la actualidad se desplaza unos 100 metros diarios.
Ya que una brújula siempre indicará el polo norte magnético es conveniente conocer la relación o diferencia existente entre el norte indicado por la brújula y el norte verdadero o geográfico. Este concepto es la declinación magnética.
La declinación magnética (“variación” en navegación aeronáutica) es el ángulo comprendido entre el norte verdadero (geográfico) y el norte magnético, es decir es el ángulo de diferencia que existe entre el norte geográfico y el norte que marcará una brújula.
Más información en este enlace Declinación magnética
Conceptos de navegación. Curso y rumbo
Llamaremos curso (course) a la trayectoria a seguir, es el recorrido planificado o deseado entre dos puntos A y B. Se podría identificar como la línea recta que une ambos puntos.
Más información en este enlace Conceptos de navegación. Curso y rumbo
Tipos de mapas
Se pueden clasificar los mapas atendiendo a diferentes criterios, en nuestro caso los clasificaremos según el contenido y el modo de representación.
Más información en este enlace Tipos de mapas
Proyecciones cartográficas
Un mapa es una representación de dos dimensiones de la tierra, que tiene tres dimensiones, el paso de una representación de tres dimensiones a dos dimensiones se conoce como proyección.
Más información en este enlace Proyecciones cartográficas
Nubes
Las nubes pueden darnos valiosa información, vamos a repasar los diferentes tipos de nubes que podemos encontrar en nuestras salidas.
Más información en este enlace Tipos nubes
GPS (Sistema de Posicionamiento Global) y otros Sistemas de Posicionamiento Global
GPS (Global Positioning System) Sistema de Posicionamiento Global
Es un sistema que permite localizar un objeto que esté sobre la Tierra con una alta precisión. Para ello el dispositivo receptor localiza al menos cuatro satélites de la red de satélites colocados en órbita, de los que recibe unas señales que le indican la identificación y la hora del reloj interno de cada satélite. Con esta información se calcula la distancia al satélite. Conociendo la distancia a esos satélites y por el método de “trilateración” el dispositivo GPS puede determinar la posición sobre la superficie de la Tierra.
Con tres satélites el dispositivo es capaz de determinar la latitud y la longitud de su posición, es decir, su posición en dos dimensiones, al añadir un cuarto satélite podrá, además calcular la altitud obteniendo la posición en tres dimensiones. Las señales que emite cada satélite forma una esfera con el satélite en el centro, el punto de intersección de todas las esferas es el que determina la posición donde se encuentra el dispositivo receptor GPS.
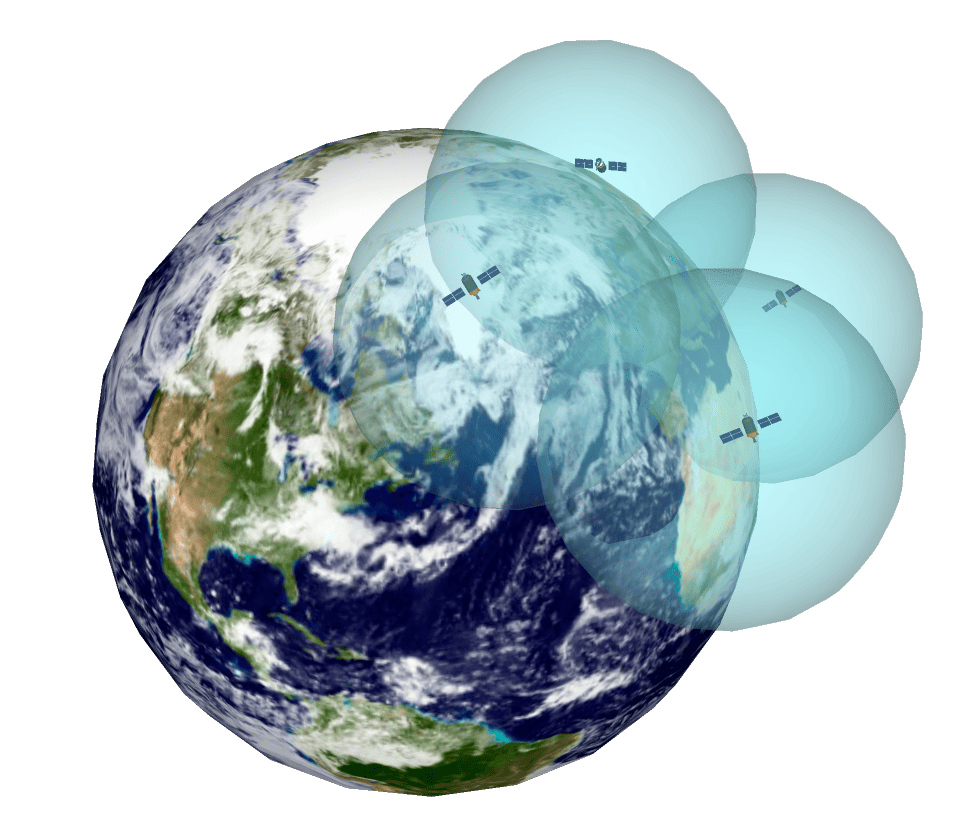
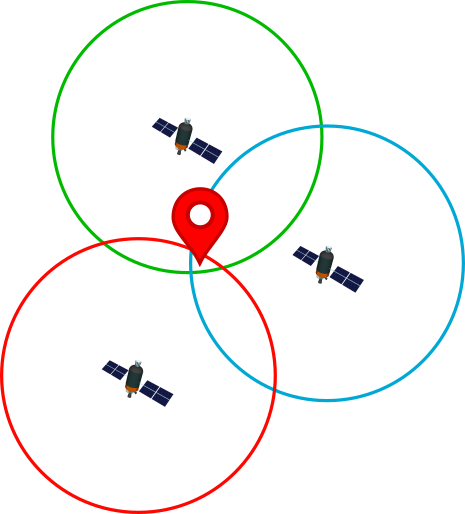
Como curiosidad, los satélites transmiten en tres frecuencias diferentes de la banda L de radiofrecuencia (1000 – 2000 MHz) del espectro electromagnético.
Otros Sistemas de Posicionamiento Global
Actualmente existen cuatro grandes sistemas de posicionamiento global:
GPS: El más conocido y utilizado actualmente es el GPS, que es un sistema propiedad del Departamento de Defensa de Estados Unidos y consta de tres partes: satélites en órbita, estaciones base y receptores. Su cobertura se extiende a todo el mundo. Su verdadero nombre es NAVSTAR (Navigation Satellite Timing and Ranging)
GLONASS (GLobalnaya NAvigatsionnaya Sputnikovaya Sistema): Es el sistema de posicionamiento propiedad del estado de Rusia y también tiene cobertura en todo el mundo.
Galileo: Galileo ha sido desarrollado por la UE como alternativa al GPS y al GLONASS.
BeiDou: Es el sistema creado por China y tiene cobertura en todo el mundo aunque ofrece mayor precisión en Asia y el Pacífico. BeiDou significa Osa Mayor en chino.
También existen otros sistemas aunque su cobertura sólo tiene ámbito regional, es el caso del sistema NavIC de India o el sistema QZSS de Japón.
Coordenadas geográficas
Coordenadas geográficas
Sistema de referencia de coordenadas angulares esféricas para representar localizaciones en la tierra. Se necesitarán al menos tres valores para representar una ubicación: una para la posición horizontal, otra para la posición vertical y una tercera que indique la distancia a la cota cero, que se identifica como la del nivel del mar. Los valores de posición horizontal y vertical se dan habitualmente en grados sexagesimales, ya que se trata de ángulos cuyo centro es el de la Tierra.
Meridianos y paralelos
Se divide la esfera terrestre con líneas imaginarias denominadas meridianos y paralelos.
Meridianos
Los meridianos son líneas que van del polo norte al polo sur. El primer meridiano, meridiano cero o meridiano de Greenwich es la línea imaginaria que une los polos norte y sur pasando por la localidad de Greenwich en Inglaterra, el resto de meridianos toman a éste como referencia. Hacia el este los meridianos van tomando valores positivos hasta los 180º mientras que hacia el oeste los valores tomados son negativos.
Paralelos
Los paralelos son líneas que van de este a oeste, son perpendiculares al eje norte-sur y son paralelas al Ecuador. El Ecuador es el paralelo "0".
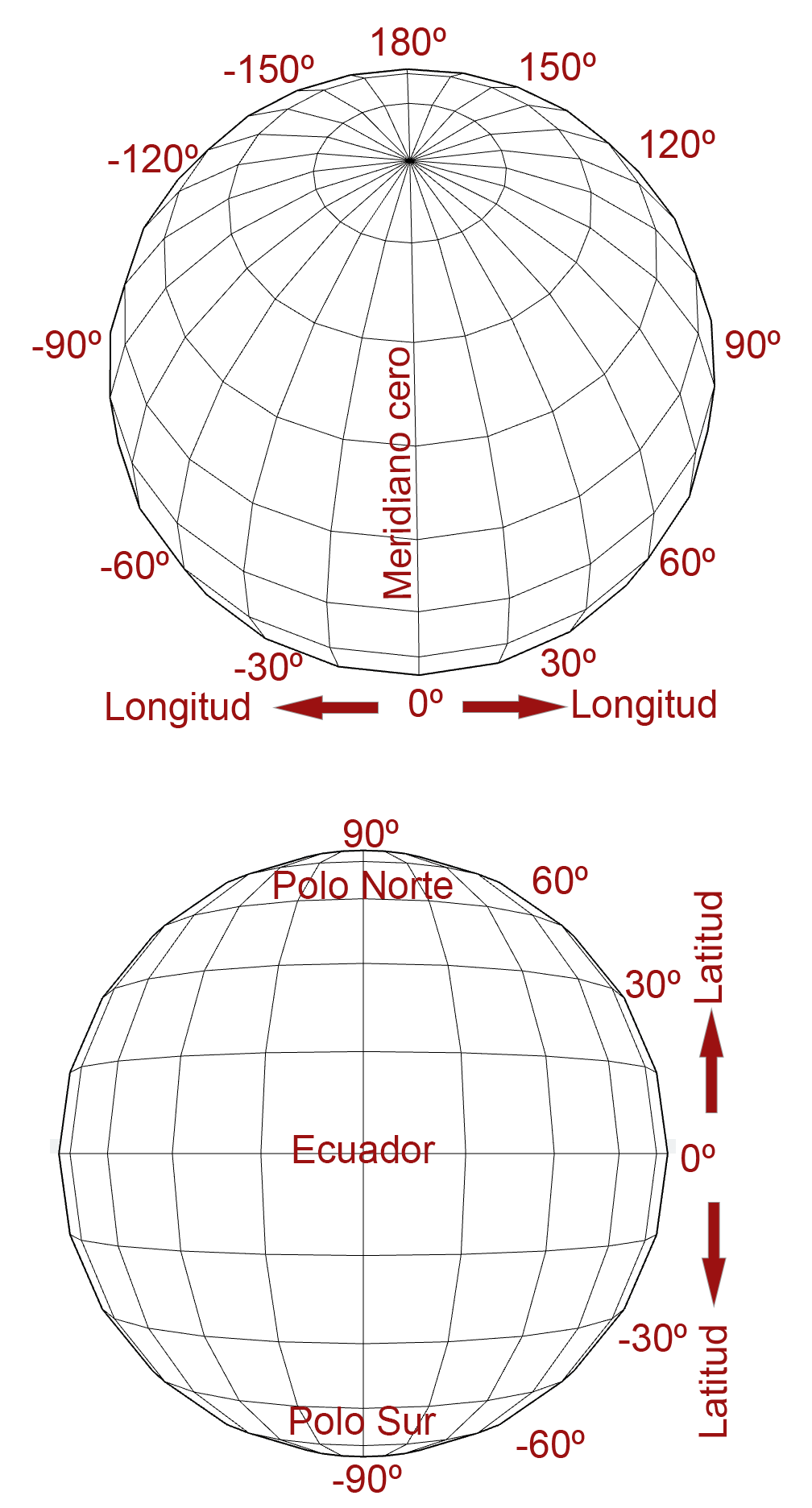
Latitud y Longitud
Latitud
La latitud de un punto sobre la superficie de la tierra es el ángulo que forma el plano que pasa por el ecuador y la línea que pasa por el punto y el centro de la Tierra. Todos los puntos con la misma latitud forman círculos imaginarios que son “paralelos” entre sí y paralelos al ecuador, que es el mayor de los “paralelos”.
Longitud
La longitud de un punto sobre la superficie de la tierra es el ángulo que forma el plano que pasa por el meridiano de Greenwich, con el plano del meridiano que pasa por el punto. Todos los puntos con la misma longitud forman semicírculos que pasan por los polos semejantes a los gajos de una naranja.
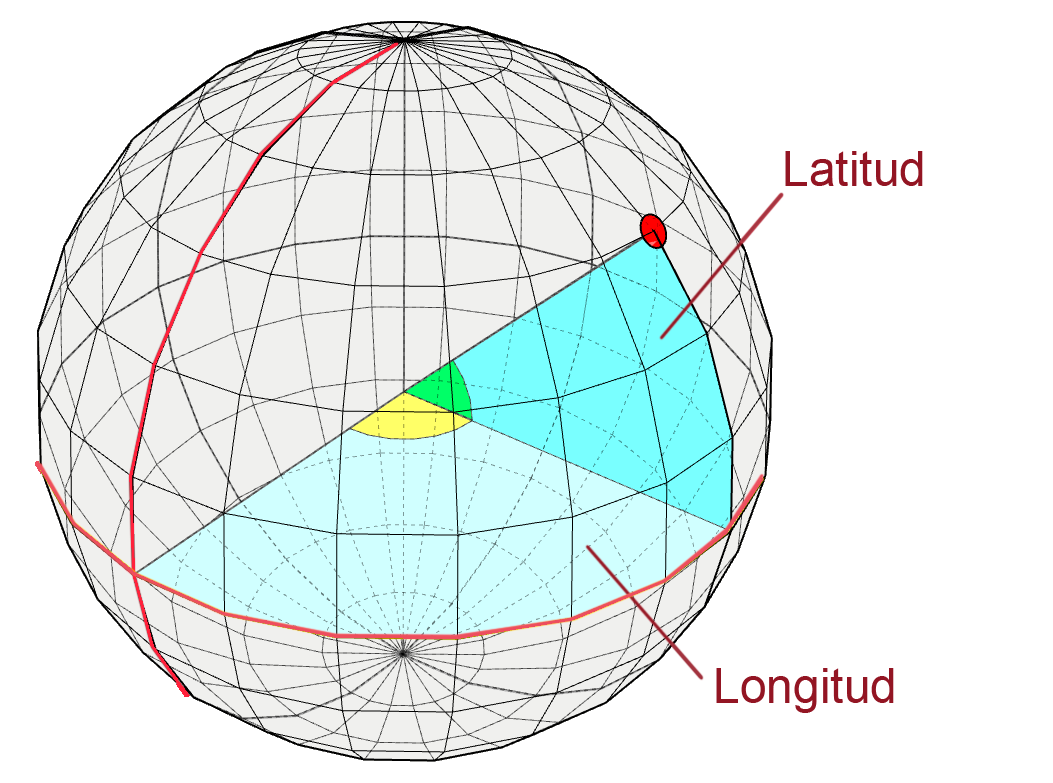
Nociones básicas sobre interpretación de mapas
Representación de datos geográficos en dos dimensiones, curvas de nivel
Para la representacion de la distribución de una variable (temperatura, presión atmosférica...) sobre una superficie se utilizan isolíneas. Las isolíneas son líneas que unen puntos con igual valor en la superficie, el valor puede ser aquel que se escoja, temperatura (isotermas), presión (isobaras), precipitación (isoyetas).
Las isolíneas que unen puntos de igual altitud del terreno se conocen como "curvas de nivel" y permiten la representación de la superficie del terreno en dos dimensiones.

Tipos de curvas de nivel
En los mapas cartográficos encontraremos representadas dos o tres tipos de curvas de nivel, normalmente en color marrón.
Curvas de nivel
Las curvas de nivel son las líneas más finas.
Curvas de nivel maestras
Son las líneas más gruesas.
Curvas de nivel auxiliares
Son líneas más finas y discontínuas.
Información numérica adicional
En las curvas maestras se muestra un número que representa el valor absoluto de altitud a lo largo de esa línea. Los números están orientados de forma que la parte superior del número indica en qué dirección aumenta el valor de altitud.
Si entre dos líneas maestras, por ejemplo de 900 y 950, encontramos cuatro curvas de nivel, estas dividirán el espacio en 5 partes y las interpretaremos como los valores intermedios entre 900 y 950, es decir: 910, 920, 930 y 940.
Si una línea maestra no presenta indicación con número, probablemente por falta de espacio en la visualización, interpretaremos que sigue el mismo intervalo que para el resto de líneas maestras.
Las cumbres o cimas son los puntos del terreno de máxima altitud relativa y también se muestran en el mapa. En el ejemplo siguiente podemos ver que existen varias cumbres (indicadas por un punto y números en color negro) de 999, 984, 883, 887, 1051... metros.
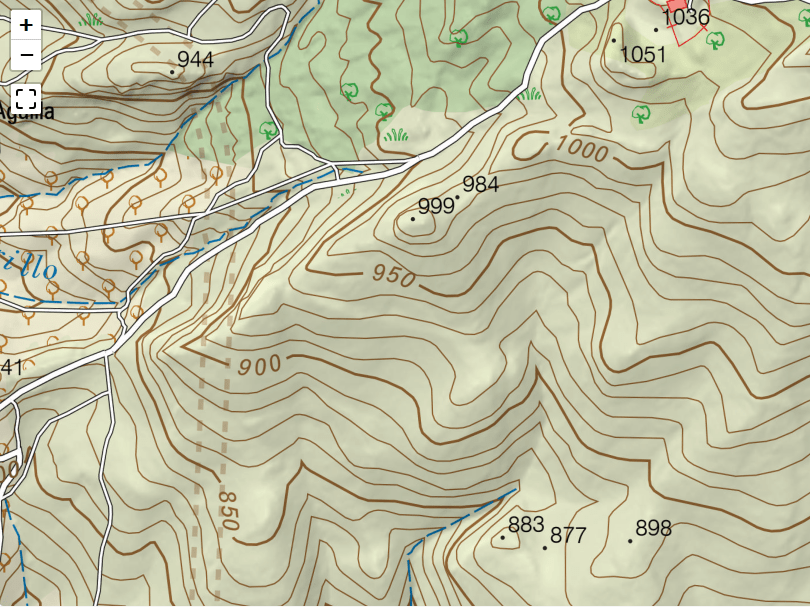
Más información
El gradiente
El gradiente o grado de variación de la altitud es siempre perpendicular a la curva de nivel. Cuando las líneas están muy cerca unas de otras nos indican que la variación de altitud es muy rápida lo que significa que la altitud aumenta o disminuye acentuadamente.
La distancia entre curvas de nivel dependerá de la escala del mapa y suele estar entre 50 y 100 metros para las líneas maestras y entre 10 y 20 metros para las líneas intermedias (más finas).
La escala
La escala de un mapa indica la equivalencia entre la distancia real y la distancia representada en el mapa. Por ejemplo, una escala de 1:10.000 significa que un metro en el mapa equivale a 10.000 metros en la realidad o que un centímetro en el mapa equivale a 10.000 centímetros en la realidad. Escalas más grandes cubriran una mayor superficie del terreno pero el detalle será menor.
La leyenda
Si el mapa tiene una leyenda o documentación de la simbología utilizada es conveniente repasarla pues nos aportará mucha información acerca de las unidades de medida empleadas, los colores, orientación, escala y elementos representados.
En el mapa de la imagen anterior podemos ver que existen algunos arroyos o rios no permantenes marcados con trazo azul discontínuo

también un olivar en el margen izquierdo, por debajo (a menor altitud) de una zona frondosa y zonas de matorral.


Declinación magnética
Concepto de declinación magnética
El campo magnético generado por la Tierra no es inmutable, por el contrario, varía constantemente tanto en su posición como en su intensidad y además, periódicamente (en ciclos de miles de años) se invierte. En la actualidad se desplaza unos 100 metros diarios.
Ya que una brújula siempre indicará el polo norte magnético es conveniente conocer la relación o diferencia existente entre el norte indicado por la brújula y el norte verdadero o geográfico. Este concepto es la declinación magnética.
La declinación magnética (“variación” en navegación aeronáutica) es el ángulo comprendido entre el norte verdadero (geográfico) y el norte magnético, es decir es el ángulo de diferencia que existe entre el norte geográfico y el norte que marcará una brújula.
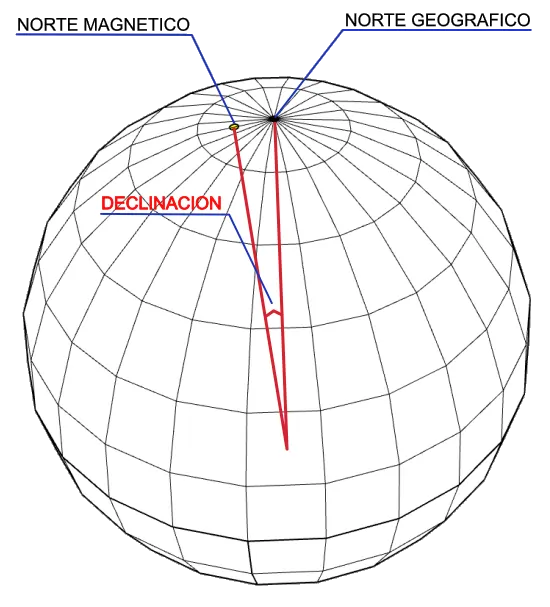
La declinación magnética dependerá la posición en la tierra desde donde se mida, siendo cero en el punto de la tierra en el que estén alineados.
En la figura siguiente se muestra la declinación para tres puntos A, B y C situados en posiciones diferentes sobre la superficie terrestre. Para el punto C la declinación es cero ya que está alineado con el polo norte geográfico y el polo norte magnético.
La declinación se considera positiva si el norte magnético se encuentra al este del norte geográfico y negativa si el norte magnético se encuentra al oeste del norte geográfico.
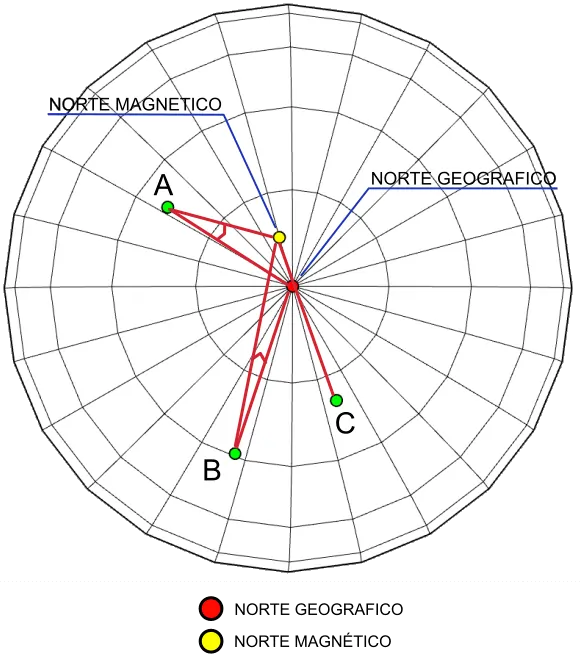
Mapas de declinación magnética
Para conocer la variación magnética en cualquier punto del planeta se elaboran mapas donde se indica la declinación magnética en cada ubicación por medio de isolíneas que representan un ángulo específico, al tratarse de isolineas que representan ángulos se las llama isógonas. Conocida nuestra posición o la posición de la ruta se tomará como referencia la línea isogónica más cercana a nuestra posición.
La línea isogónica especial que une puntos de variación “0º” se denomina línea agónica (sin ángulo). Una brújula situada en una posición correspondiente a una curva agónica apunta exactamente al norte verdadero, pues su declinación magnética será nula.
Map developed by NOAA/NCEI and CIRES
https://ngdc.noaa.gov/geomag/WMM
Published December 2019
Ira a Sicami Sicami Tracks
Tipos de Mapas
Tipos de mapas. Criterios de clasificación
Los mapas se pueden clasificar los mapas atendiendo a diferentes criterios, en nuestro caso los clasificaremos según el contenido y el modo de representación.
Mapas según el tipo de contenido
Dependiendo del modo de representación del terreno podemos distinguir entre:
Mapas raster
Los mapas "raster" consisten en imágenes georreferenciadas, es decir, es un archivo de imagen al que se le asignan coordenadas para que se muestre en la ubicación correcta al abrirlo con una aplicación. Se pueden construir con formatos de imagen estándar (jpg, bmp…) acompañados de un archivo de calibración, aunque existen formatos específicos para cartografía digital
Los mapas de este tipo pueden ocupar mucho espacio en memoria por lo que suelen estar disponibles como mapas mosaicos en el que el mapa total se divide en piezas más pequeñas (teselas) para manejar únicamente las partes del mapa correspondientes a la zona que se vaya a utilizar.
Mapas vectoriales
Este tipo de mapas está compuesto por objetos vectoriales como polilíneas, polígonos o puntos que contienen información adicional como color, etiquetas, tipo de terreno. Estos elementos y otra información se distribuirán en capas que se mostrarán según la configuración de opciones de visualización o el nivel de zoom. Estos mapas pueden contener información que permita a una aplicación el cálculo automático de rutas.
DEM: Modelo Digital de Elevaciones
Son mapas que contienen solamente información sobre altitud del terreno. Normalmente se utilizarán en combinación con otro mapa para representarlo en 3D y asignar altitud a los puntos de una ruta y waypoints. (Ver sección "Información sobre métodos de cálculo de datos" en este sitio)
Mapas según el modo de representación del terreno
Según el modo de representación del terreno podemos distinguir entre:
Mapas topográficos
El mapa topográfico es de tipo raster o vectorial y representa el terreno mediante curvas de nivel, colores y símbolos gráficos para mostrar información sobre la zona como accidentes geográficos, caminos, senderos, fuentes…
Ortofotos
Las ortofotos son mapas tipo raster consistentes en imágenes aéreas del terreno con proyección ortogonal (perpendicular a la superficie). Para evitar distorsiones debidas al punto de vista de la cámara, las fotografías aéreas se rectifican para adaptarlas a la forma del terreno.

Mapas de carreteras
Los mapas de carreteras son mapas vectoriales especialmente orientados a la navegación urbana e interurbana. Se destacan elementos útiles para el automovilista o usuario de la vía.
Las proyecciones cartográficas
Proyecciones cartográficas
Un mapa es una representación en dos dimensiones de la tierra, que tiene tres dimensiones.
El paso de una representación de tres dimensiones a dos dimensiones se conoce como proyección.
Para que exista una correspondencia entre los puntos de la superficie curva de la tierra y los de la superficie plana de un mapa se usa una malla con coordenadas "x" e "y" obtenidas de las coordenadas de longitud y latitud mediante diferentes cálculos matemáticos.
Esto provoca que inevitablemente haya una deformación al realizar la proyección, por lo que será en función de cuales sean los parámetros que queramos leer (distancias, superficies o ángulos) se utilizará uno u otro de los sistemas de proyección disponibles, siendo imposible una proyección que represente correctamente los tres simultáneamente.
En función de esto podemos distinguir tres tipos de proyección.
Proyecciones según conservación de distancias, superficies o ángulos
Proyección equidistante:
donde se conservan las distancias
Proyección equivalente:
donde se conservan las superficies
Proyección conforme:
donde se conserva la forma o relación de ángulos entre puntos.
Para mejorar el resultado de las proyecciones se pueden emplear superficies geométricas que posteriormente se abatirán en el plano. Veamos algunas de las más habituales:
Proyecciones sobre superficies geométricas
Proyección cilíndrica.
Se obtiene colocando un cilindro tangente a la esfera terrestre en el Ecuador. La proyección de Mercator es la proyección cilíndrica más conocida. Los meridianos y paralelos quedarán perpendiculares en la proyección, la distancia entre los paralelos aumentará conforme aumenta la latitud. Esto producirá una deformación más grande cuánto más alejada esté la posición norte o sur respecto al Ecuador. El Ecuador será la única línea donde se conservará la escala. Los territorios y países situados más al norte aparecerán representados con un tamaño mayor al real y los polos no se representan pues estarían en el infinito. Aunque este sistema provoca que se distorsionen mucho las áreas cercanas a los polos es útil para la navegación ya que es un tipo de proyección “conforme”, es decir, que conserva la relación angular entre puntos.
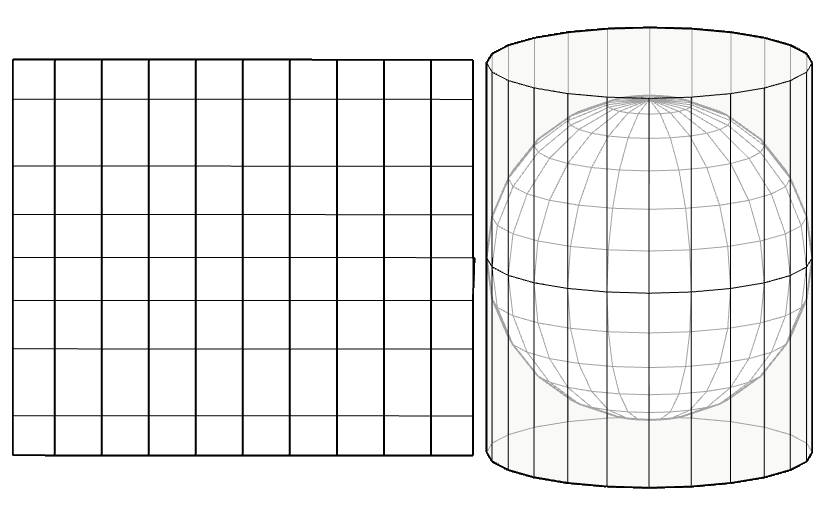
Proyección Transversa de Mercátor
La Proyección Transversa de Mercátor es una variante de la proyección de Mercator donde se expanden los meridianos hacia el este u oeste del meridiano de Greenwich. Los meridianos se representan por líneas curvas paralelas entre sí y convexas hacia el Ecuador. En este caso las distorsiones son mayores cuanto más lejana esté la posición respecto al meridiano de Greenwich y éste será la única línea donde se conservará la escala.
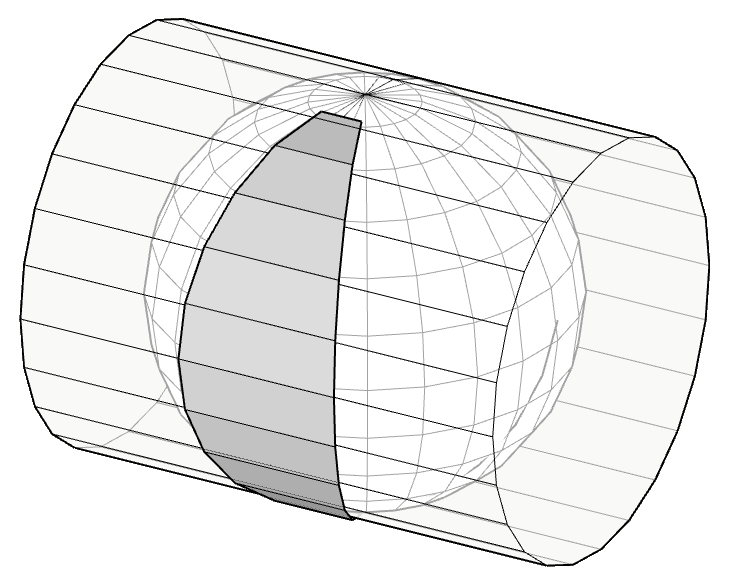
La Proyección Universal Transversa de Mercátor (U.T.M.)
La Proyección Universal Transversa de Mercátor (U.T.M.) es otro sistema de proyección, basado en la proyección transversa, que divide el globo terráqueo en 60 sectores o husos a lo largo del Ecuador (cada sector cubre 6 grados de longitud). Cada zona tiene un meridiano central y la intersección de este meridiano central con el Ecuador se establece como origen “x” e “y” de la zona.
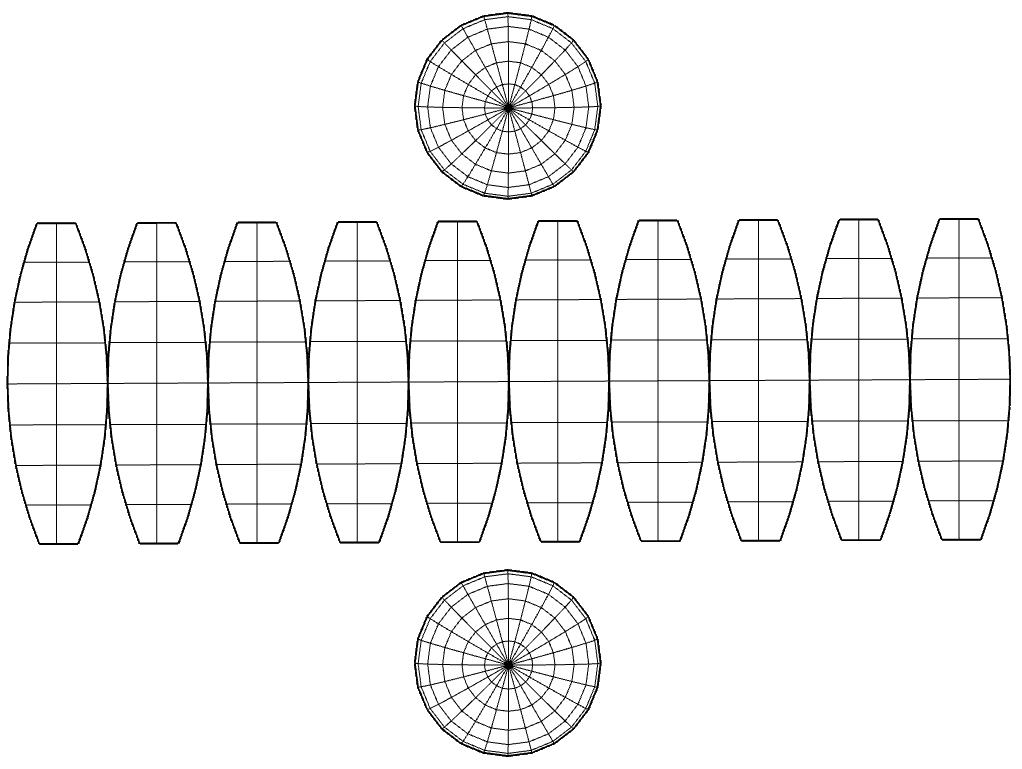
Proyección cónica
Se proyectan meridianos y paralelos sobre una superficie cónica tangente con el vértice del cono en el eje formado por los polos. Los meridianos se transformarán en líneas rectas partiendo del polo y los paralelos se convertirán en circunferencias concéntricas centradas en los polos.
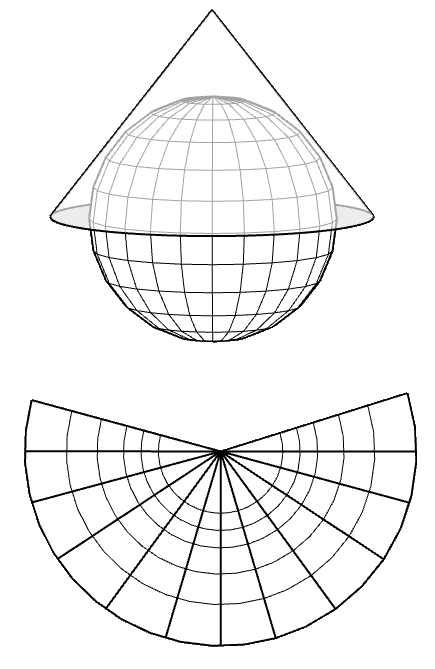
Nubes
Tipos de nubes según sus formas, colores y altitud.

Nubes altas (por encima de los 6.000 metros)
Cirros:
Blancas, algo transparentes, no tienen sombras interiores ni proyectan sombra sobre el suelo. Forman filamentos largos y delgados en ocasiones alineados como mechones de pelo. Están formados mayormente por cristales de hielo y suelen producir halos con el sol o la luna. Con cirros escasos y finos el tiempo será estable, pero probablemente tenderá a empeorar si comienzan a adquirir volumen y densidad.
Cirrocúmulos:
Parecidos a los cirros pero de mayor densidad formando una capa casi contínua con formas redondeadas. Tampoco presentan sombras interiores y son completamente blancos. Suelen anticipar la llegada de un frente frío. También pueden formar halos.
Cirrostratus:
Aparece como una capa blanca y transparente a modo de velo que cubre parte del cielo sin una estructura clara. Suelen presentar estriados alargados y de cierta anchura. Forman halos. Suelen aparecer antes de un aumento grande de nubosidad y empeoramiento del tiempo.
Nubes medias (entre 2.000 y 6.000 metros)
Alto cúmulos:
Son de color blanco y gris azulado. Con sombras interiores. Están formadas por agua y hielo. Son más densas y compactas y de aspecto variado, lenticulares, globulares, estratiformes. No producen precipitación, pero anticipian la llegada de mal tiempo por tormentas.
AltoStratos:
Forma una lámina de color gris o azulada y translúcida con nubes densas mezcladas con zonas más finas. Permiten el paso del sol que aparecerá como un disco luminoso. Suelen ser presagio de lluvia fina y descenso de temperatura.
Nimbostratos:
De color gris oscuro con zonas más o menos opacas. Bloquean al sol completamente. Dan precipitaciones con bastante probabilidad de carácter leve o moderado tanto de lluvia como de nieve.
Nubes bajas (entre 0 y 2.000 metros)
Estratocumulos:
De color blanco con zonas de color gris de diferentes intensidades. Tamaño grande y con desarrollo vertical notable. Este tipo de nubes no suele provocar precipitaciones.
Estratos:
De color gris y poco definidas, parece niebla ya que están a poca altura del suelo pudiendo provocar una llovizna ligera.
Cumulonimbos:
Son nubes de gran desarrollo vertical, pudiendo cubrir desde el nivel más bajo hasta el más alto. Son densas y su parte superior se extiende a veces en un gran penacho siendo la parte inferior de color oscuro. Suele producir chubascos y tormentas eléctricas. Está compuesto de gotas de agua de gran tamaño y cristales de hielo en su parte superior.
Cúmulos:
De gran tamaño, base aplanada y con grandes protuberancias en la parte superior. Color blanco con abundantes sobras. Suelen ser típicos en tiempo estable y soleado y no presentan riesgo de precipitación aunque pueden crecer hasta formar cumulonimbos cuando existen corrientes ascendentes fuertes y alta humedad.
Altitud, Altura y Elevación
Altitud, Altura y Elevación
Es común utilizar indistintamente los términos altitud y altura para referirnos a una ubicación. A continuación vamos a recordar la definición de estos términos.
La altura es la distancia vertical de un cuerpo hasta la superficie terrestre (el suelo o el mar).
La altitud es la distancia vertical de un cuerpo hasta el nivel del mar, independientemente de que el objeto esté sobre la superficie de la tierra o por encima de ella (avión, dron, ...)
La elevación es la distancia vertical hasta el nivel del mar de un punto que está sobre la superficie terrestre y en contacto con ella.
En siguiente gráfico, vemos que el punto verde está situado a cierta altitud y a cierta altura, mientras que el punto amarillo sobre la superficie del terreno está a cierta altitud, pero su altura es cero ya que está tocando el suelo. El terreno sobre el que está situado está a una determinada elevación.
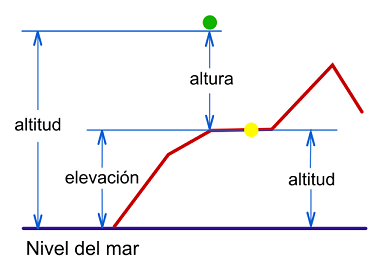
En determinados casos los valores pueden coincidir, aunque nos estaremos refiriendo a conceptos diferentes. Por ejemplo, para el punto amarillo la elevación coincide con la altitud y si el cuerpo estuviera volando sobre el mar, su altitud coincidiría con su altura.
Desniveles y pendientes
Desniveles y pendientes de una ruta. Desnivel positivo, negativo y acumulado.
El desnivel, por definición, es la diferencia de altura entre dos o más puntos. El punto de nivel cero será el punto donde comencemos la ruta, independientemente de la altura de ese punto al nivel del mar.
El desnivel acumulado será positivo si la altura final es mayor que la del punto de partida (hemos acumulado metros ascendiendo) y negativo si la altura final es menor que la del punto de partida (hemos acumulado metros descendiendo). Si el punto de partida y el punto final coinciden, el desnivel acumulado será cero.
Estrictamente, para calcular el desnivel acumulado de una ruta, sumaremos el desnivel positivo y el desnivel negativo. Por ejemplo, en una ruta circular que sube un puerto de 500 metros y que tiene el mismo punto de salida y llegada, el desnivel positivo será de 500 metros y el negativo de otros 500 metros con lo que el desnivel acumulado será de 1000 metros. En cualquier ruta con el mismo punto de partida y llegada el desnivel acumulado positivo será igual al desnivel acumulado negativo.
Como habitualmente las rutas no suelen ser solo de subida o bajada, sino que hay tramos de ascenso y tramos de descenso concatenados, el desnivel acumulado positivo será la suma de todas las ganancias de altura y el negativo el de todas las pérdidas de altura. Por lo que no coincidirá con la altura ganada o ganancia de altitud total que es la diferencia entre la cota más alta y la cota más baja de la ruta.
Ejemplo: Salimos del punto A con altitud 500 metros sobre el nivel del mar y finalizamos en el punto F con altitud 600 metros sobre el nivel del mar, pasando por los puntos intermedios B, C, D y E.
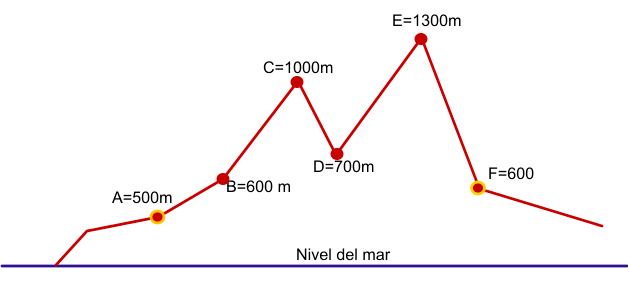
Sumamos todas las ganancias de altitud en los tramos ascendentes:
A-B: 600-500 = 100
B-C: 1000-600 = 400
D-E: 1300-700 = 600
Desnivel acumulado positivo: 1.100 metros
Sumamos todas las pérdidas de altitud en los tramos descendentes:
C-D: 700-1000 = -300
E-F: 600-1300= -700
Desnivel acumulado negativo: -300 – 700 = -1.000 metros
Desnivel acumulado total: 1.100-1000 = 100 metros.
En ciclismo cuando se habla de “desnivel acumulado” se suele hacer referencia al desnivel positivo, ya que da una mejor idea de la dificultad de la ruta.
Pendientes de una ruta
Para determinar la dificultad de una ruta tan importante como conocer los desniveles es conocer las pendientes de las diferentes rampas. La pendiente es la relación entre la distancia ascendida en vertical y la distancia horizontal recorrida para ascenderla. Una formula rápida y sencilla para calcular la pendiente media de un tramo sería la siguiente siempre que se conozcan la distancia vertical y la distancia horizontal al punto de ascenso:
Pendiente (%) = Distancia vertical x 100 /Distancia horizontal
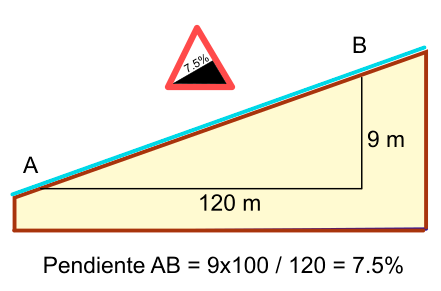
Según los datos conocidos: distancia recorrida, ángulo de elevación, distancia vertical, etc. existen otros métodos en los que se aplican cálculos trigonometrícos.
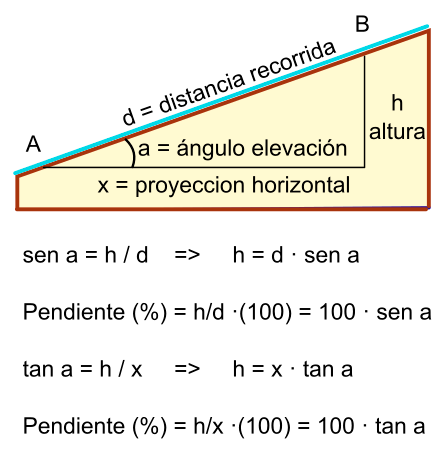
La Ley de Weigner o supercompensación
La Ley de Weigner o principio de supercompensación
Cuando realizamos ejercicio físico o cualquier tipo de esfuerzos continuados y repetidos en el tiempo, nuestro cuerpo sufre una serie de adaptaciones que producirán una mejora de nuestra fuerza y rendimiento. Es la forma en la que se preparará para enfrentar esfuerzos similares o superiores en el futuro minimizando los posibles daños.
Este proceso no es instantánedo, requiere de un tiempo de reparación y regeneración. Al aplicar un estímulo, esfuerzo o carga de trabajo sufriremos una disminución inicial de nuestro rendimiento o capacidad de esfuerzo como consecuencia del cansancio y la fatiga de nuestras fibras musculares. Tras el descanso, indispensable en cualquier plan de entrenamiento, se producirá un proceso de recuperación que, no solo nos devolverá al nivel de rendimiento previo al ejercicio, si no que hará que aumente. Si el esfuerzo no se vuelve a repetir, el nivel de rendimiento volverá a descender ya que nuestro organismo siempre tenderá al ahorro energético.
Gráficamente podríamos representarlo como sigue:
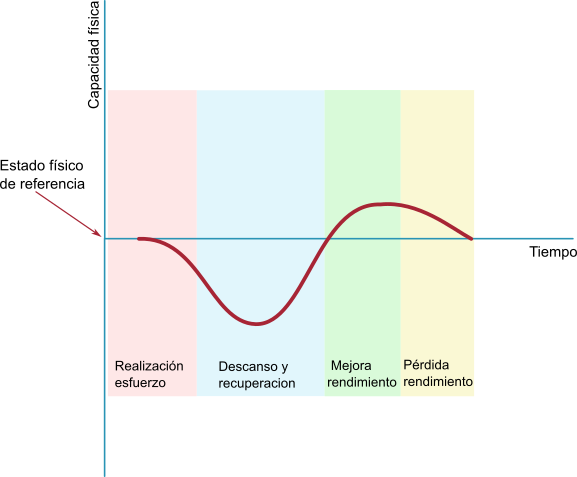
Obviamente un esfuerzo puntual no será suficiente para que se produzca ninguna mejora y será necesaria la repetición de los esfuerzos (entrenamientos) para que el estado de forma adquirido no solo no se pierda si no que mejore. En definitiva, es necesaria la acumulación de estímulos para conseguir la mejora del rendimiento.
El principio de supercompensación o ley de Weigner nos muestra cómo evolucionaría nuestra condición física con la acumulación de entrenamiento.
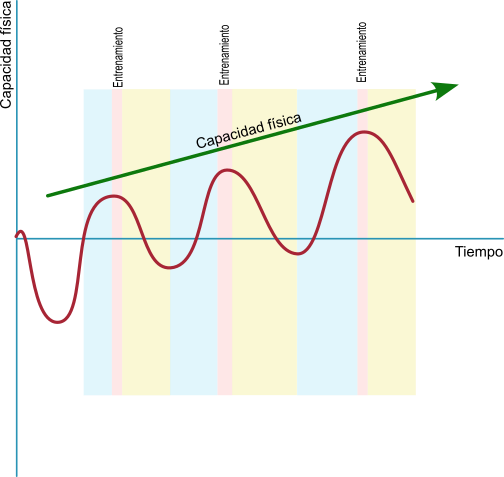
Por otro lado los entrenamientos deben ir incrementando su intensidad y/o duración para que no se produzca un estancamiento de la evolución.
Otra conclusión evidente a la vista del gráfico, es que el descanso y la correcta recuperación son indispensables para obtener los resultados deseados, permitiendo al organismo la reparación de los tejidos dañados y las adaptaciones físicas y metabólicas necesarias.
Curva y perfil de potencia en ciclismo
Curva y perfil de potencia en el ciclismo
El perfil de potencia en ciclismo es una representación gráfica de los valores de potencia media que obtiene el deportista durante determinados periodos de tiempo realizando un esfuerzo.
Por potencia media entendemos la media arimtética de la potencia generada en un periodo de tiempo y se obtendrá divididiendo los vatios de toda la sesión entre el tiempo empleado. Normalmente es un dato que facilitará automáticamente el potenciómetro.
Por lo general se utilizan ciertos periodos de tiempo determinados o críticos porque aportarán información correspondiente a distintas capacidades físicas que desarrollaremos en otro artículo, los más característicos son:
Potencia en 5 segundos: indica la capacidad para esfuerzos máximos o capacidad anaeróbica máxima.
Potencia en 1 minuto: indica la capacidad anaeróbica.
Potencia en 5 minutos: indica la Potencia Aeróbica Máxima (PAM) o consumo máximo de oxígeno (VO2max)
Potencia en 20 minutos: indica la potencia en las proximidades del umbral anaeróbico
Potencia en 60 minutos: También conocida como Umbral de Potencia Funcional o FTP. Es un indicador de la potencia máxima que seríamos capaces de desarrollar durante un periodo de una hora.
Sin entrar en describir los sistemas energéticos que utiliza el organismo para suministrar energía a los músculos nos limitaremos a describir someramente algunos de los conceptos mencionados:
Esfuerzo aeróbico y anaeróbico
Llamaremos esfuerzo de caracter aeróbico a aquel esfuerzo de duración prolongada en el tiempo y que se realiza a una intensidad moderada o baja y por tanto sostenible. El sistema circulatorio es capaz de aportar oxígeno suficiente para las reacciones químicas celulares productoras de energía.
Por otro lado, se conoce como esfuerzo de caracter anaeróbico a aquel que tiene una intensidad alta y que se realiza durante un periodo de tiempo corto. Debido a que este esfuerzo es muy intenso, el oxígeno disponible para las células es limitado al excederse la capacidad de suministro del sistema circulatorio, por lo que el sistema de producción de energía en las células será diferente. Estos esfuerzos solo serán sostenibles durante periodos de tiempo cortos.
Volúmen máximo de oxígeno
El VO2máx es el "Volúmen de Oxígeno máximo" y representa la cantidad máxima de oxígeno en mililitros que una persona consume cada minuto y por cada kilogramo de peso corporal (ml/kg/min) y da una idea de la eficiencia con la que nuestro cuerpo utiliza el oxígeno. Es por tanto una medida de nuestra capacidad aeróbica y de la resistencia de nuestro sistema cardiovascular. Es un valor que tiene una gran dependencia genética aunque es posible su mejora dentro de ciertos límites.
Volviendo al tema de la curva de potencia, existe software específico para entrenamiento que proporcionan automáticamente esta curva y también existe abundante literatura acerca de su interpretación, de los métodos para la obtención de los datos, etc. En esta ocasión solo queremos exponer cuál es la base para la elaboración del perfil de potencia de forma manual y sencilla para que conozcas sus fundamentos.
Es necesario señalar que, para poder comparar correctamente las curvas de distintos deportistas, o las tuyas propias a lo largo del tiempo, lo correcto sería disponer de los datos de potencia en función del peso corporal del individuo ya que no es lo mismo desarrollar 300 vatios pesando 50 kilos que desarrollar 300 vatios pesando 80 kilos, en especial cuando se trate de ascensos, para el caso del deportista más pesado, su velocidad de ascenso será menor a igual potencia desarrollada. Esta potencia por kilo se obtiene simplemente dividiendo los vatios absolutos entre los kilos de peso del deportista.
Elaboración del perfil de potencia de un ciclista
Para la elaboración de un perfil de potencia bastará con obtener la potencia media desarrollada en los diferentes intervalos de tiempo de medición.
Ejemplo: Crearemos una tabla con los valores de potencia media obtenidos en los distintos intervalos de tiempo.
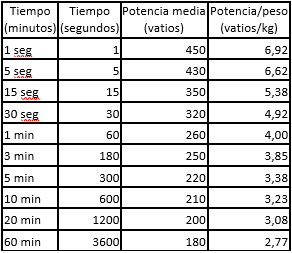
Construiremos la gráfica donde en el eje x representaremos el tiempo y en el eje y la potencia.
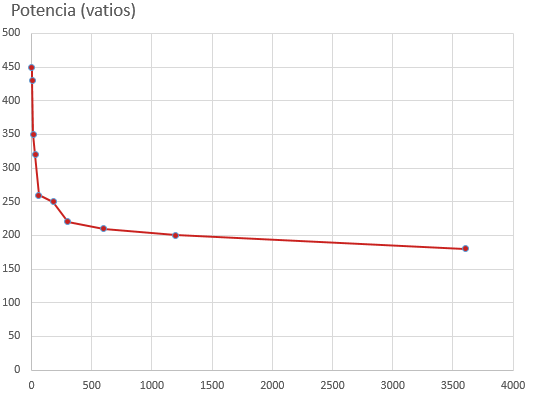
Para que la gráfica muestre de forma más detallada los valores para intervalos de tiempo más pequeños, 1 segundo, 5 segundos... que quedan muy apilados, será conveniente representar el eje x en escala logarítmica.
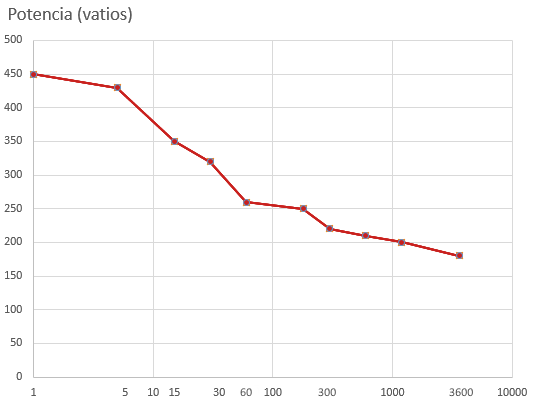
En otro artículo haremos un análisis más detallado de la información que nos suministra el perfil de potencia acerca de las capacidades del deportista y sobre todo, de las áreas donde es posible la merjora según cuales sean sus objetivos.
BCD o diámetro del círculo de pernos de los platos de una bicicleta
BCD o diámetro del círculo de pernos de los platos de una bicicleta
El BCD (Bolt Circle Diameter) o diámetro del círculo de pernos de un plato de la transmisión de una bicicleta, es el diámetro del círculo imaginario que pasa por el centro de los orificios para los pernos, siempre que éstos estén dispuestos siguiendo un patrón circular y equidistante.
Medidas habituales en el ciclismo de montaña son los BCD 104 y BCD 94 y BCD 96 y se presentan con cuatro o cinco orificios.
Cuando el plato tiene cuatro orificios, obtener su BCD es tan sencillo como medir la distancia entre los centros de dos orificios opuestos.
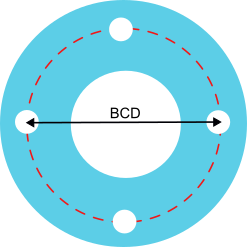
Cuando el plato tenga cinco orificios el proceso será algo más complicado, pero no excesivamente. En este caso tomaremos la medida, en milímetros, de la distancia entre los centros de dos orificios contiguos y realizarremos el siguiente cálculo:
56 x distancia-centros / 32,9.
Por ejemplo, si la medida es de aproximadamente 55 mm (será difícil encontrar el centro exacto del orificio), tendremos: .
56 x 55 / 32,9 = 93,6 que podemos redondear a 94, con lo que el BCD será 94.
Fundamentos matemáticos y método de cálculo para cualquier distribución
Para los que tengan curiosidad acerca de donde sale la fórmula anterior y que además quieran poder calcular el BCD de cualquier distribución regular y circular de tornillos, pernos o sus orificios, no es necesaria más que la aplicación de trigonometría básica.
Sabiendo que la circunferencia tiene 360º, si el plato tiene 5 agujeros equidistantes, el ángulo formado entre dos cualesquiera de esos agujeros será el que resulte de dividir 360 entre 5, es decir, 72º
Observando la siguiente figura vemos que podemos obtener todos los elementos necesarios para nuestro cálculo:
Por un lado tenemos el radio de la circunferencia, tomado desde el centro del disco hasta el centro del orificio. Utilizaremos este segmento como hipotenusa del triángulo rectángulo.
Por otro lado tenemos el ángulo alfa formado entre dos orificios. La bisectriz de este ángulo (línea que lo divide en dos partes iguales) definirá el cateto contiguo del triángulo rectángulo y formará un ángulo con la hipotenusa de alfa / 2.
Y finalmente, vemos que la distancia entre centros de los orificios contiguos d queda también dividida por dos por la bisectriz, con lo que ahí tendremos el cateto opuesto que nos faltaba para completar nuestro triángulo rectángulo y su longitud será d / 2.
Con estos datos y sabiendo que, en un triángulo rectángulo, el seno del ángulo no recto es igual al cateto opuesto dividido entre la hipotenusa podremos realizar los cálculos que se muestran:
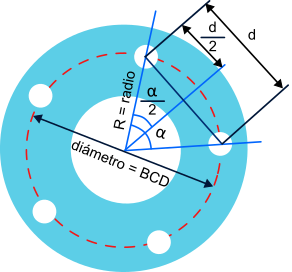
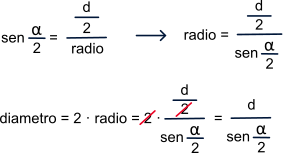
sen ( angulo / 2 ) = (distancia-centros / 2) / radio.
radio = (distancia-centros / 2) / sen ( angulo / 2 ) .
diámetro = 2 · radio .
diámetro = 2 · radio = 2·(distancia-centros / 2) / sen ( angulo / 2 ) = distancia-centros / sen ( angulo / 2 ).
Si suponemos que la medida tomada entre centros ha sido de 55 mm. podemos sustituir "distancia-centros" por esa medida:
Diámetro (BCD) = 55 / sen (36º) = 55 / 0.5878 = 93.57 aprox. 94.
La fórmula rápida que vimos anteriormente (56 x distancia-centros / 32,9 ) está basada en una relación de proporcionalidad derivada de los tamaños más pequeños de anclaje que suelen encontrarse en platos de bicicleta, que son los correspondientes a BCD 56, y con distancia entre agujeros contiguos de 32,9, pero si te fijas el cociente 32,9 / 56 = 0,5878, que es justamente el seno de 36º.
En el caso de que sean seis los orificios, el ángulo entre ellos será de 60º (360º / 6 = 60º) con lo que en nuestros cálculos para seis orificios usaremos el sen(30º) (60º / 2 = 30º), en lugar del de 36º
y el BCD se obtendrá de: BCD = distancia-centros / sen(30)
Cálculo de elevación y desnivel
Cálculo de elevación y desnivel. Desnivel positivo acumulado y desnivel negativo acumulado. Altímetros GPS, altímetros barométricos y Modelo Digital de Elevaciones DEM
Seguramente, durante una salida o después de hacerla, cuando tomamos ese apreciado café o cerveza con los compañeros, has vivido esta conversación: "yo tengo 456m de desnivel...", "pues a mi me dan 537...", "que va hombre!!!, si son 425!!!".
Pues sí, con la obtención de la altitud, necesaria para calcular el desnivel acumulado siempre hay controversias y diferencias.
En esta sección intentaremos explicar los diferentes métodos que normalmente se usan, tanto para la obtención de la altitud como de otros parámetros relacionados con salidas de senderismo, bicicleta, ect.
Para intentar aclararnos vamos a dar un repaso a los tres principales sistemas empleados para determinar la altitud de un punto, estos son: los altímetros GPS, los altímetros barométricos y el Modelo Digital de Elevaciones DEM.También te recomendamos echar un vistazo al artículo “Altitud, Altura y Elevación” en la sección “Información adicional, curiosidades y glosario de términos” de este sitio.
Dejamos también un enlace a este interesante artículo del blog "Explorando Oruxmaps" en el que se habla y explican los diferentes métodos en la que la aplicación Oruxmaps muestra la altitud y realiza el cálculo de los desniveles acumulados:
https://tronpoonpo.blogspot.com/2023/01/algoritmo-de-elevacion.html
Los receptores GPS, relojes GPS y ciclocomputadores suelen utilizar dos métodos para medir la altitud: la medición de altitud por GPS y los altímetros barométricos.
Altímetros GPS
Los dispositivos de gama más básica utilizan la medición de altitud por GPS. Ésta consiste en obtener el dato de altitud realizanto cálculos basados en la posición del receptor en los planos horizontal y vertical. En el plano horizontal la precisión del GPS es bastante alta, pero no tanto en el plano vertical, debido a la diferente posición relativa de los satélites respecto al receptor GPS (ver el artículo “Sistema de Posicionamiento Global” en la sección “Información adicional, curiosidades y glosario de términos” de este sitio). Otro problema que puede presentarse es la falta de datos por pérdida de cobertura GPS.
Altímetros barométricos
Los dispositivos de gama algo más alta suelen disponer de altímetros barométricos para la medición de la altitud. Los altímetros barométricos son bastante más fiables que los de medición por GPS y basan su funcionamiento en la medición de la presión atmosférica en la posición actual, que será menor conforme aumente la altura, ya que depende del peso de la columna de aire existente justo por encima. La densidad del aire y su presión varían de forma logarítmica con la altura reduciendose aproximadamente a la mitad a los 5000 metros, donde es aproximadamente de media atmósfera, es decir, la mitad de la presión a nivel del mar, que es de una atmósfera.
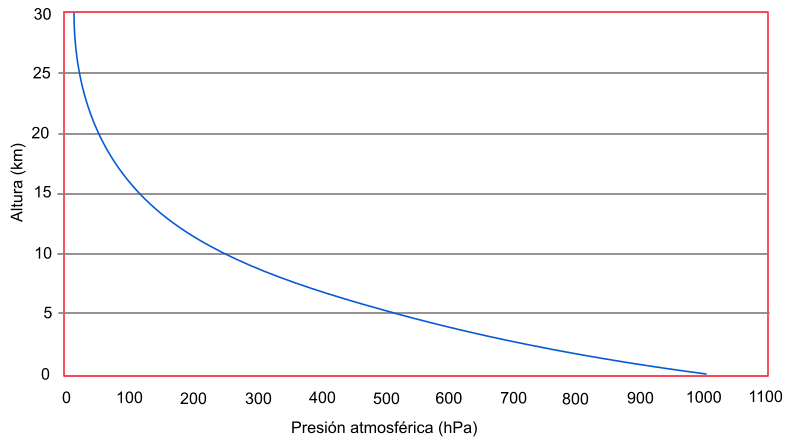
La exactitud de la medición de un altímetro barométrico depende principalmente de dos factores, el primero es la correcta calibración en el punto de partida de la actividad y el segundo, que la medición se podrá ver afectada por los cambios en la presión atmosférica que puedan provocar cambios en el clima. Un descenso de presión atmosférica provocado por una borrasca será interpretado por el barómetro como un incremento de altura. También pueden afectar otros factores como la obstrucción por suciedad del puerto del sensor.
Modelo Digital de Elevaciones (DEM)
La cartografía apoyada por mediciones satelitales, ha permitido elaborar mapas topográfícos con un elevada precisión en los datos de altitud en cada punto del terreno. Disponer de un receptor GPS con cartografía con datos DEM le permitirá calcular con mucha precisión la altitud de su ubicación. El DEM es un "raster", trama o matriz de celdas, cada celda representa una unidad de superficie cuadrada y contiene un valor numérico de altitud medido o estimado que corresponde a esa ubicación. Puede incluirse junto al mapa o ser externa. La precisión de este sistema viene limitada por un lado por la fiabilidad del propio DEM y por otro lado por la resolución de la malla empleada. En mapas es habitual utilizar DEM 200x200 metros, ya que resoluciones mayores (DEM 25x25 m, DEM 5x5 m) implican mayor cantidad de información y por tanto mayor carga de trabajo para el dispositivo, así como mayores requisitos en cuanto a la capacidad de almacenamiento interno.

Es posible aplicar correcciones a la altitud registrada por un receptor GPS utilizando el Modelo Digital de Elevaciones DEM. Es el método habitual al que suelen recurrir diferentes plataformas. En el caso de Strava en lugar de utilizar datos DEM, emplea datos de las actividades que tiene registradas, obteniendo una media de las mediciones de altitud de cada una de ellas. Cada actividad que se sube a la plataforma desde un dispositivo con altímetro barométrico se usa para desarrollar el mapa de referencia de desnivel de Strava.
A continuación mostramos un ejemplo de como puede afectar la resolución del DEM a la estimación del perfil de elevación.
En este primer caso hemos trazado una ruta utilizando un DEM con resolución de 10x10 m.
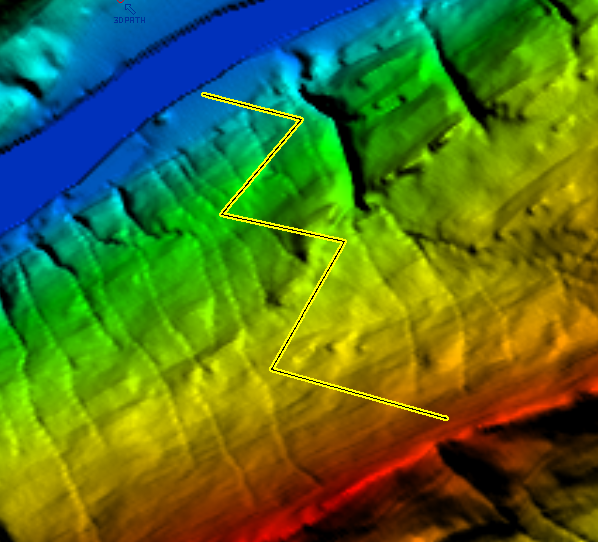
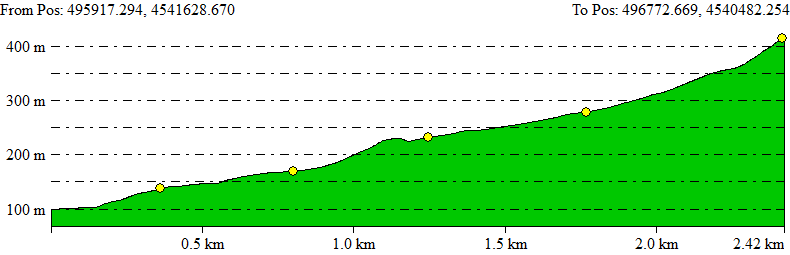
En este segundo caso se muestra la misma ruta sobre un DEM con resolución de 30x30 m.