BCD o diámetro del círculo de pernos de los platos de una bicicleta

BCD o diámetro del círculo de pernos de los platos de una bicicleta

El BCD (Bolt Circle Diameter) o diámetro del círculo de pernos de un plato de la transmisión de una bicicleta, es el diámetro del círculo imaginario que pasa por el centro de los orificios para los pernos, siempre que éstos estén dispuestos siguiendo un patrón circular y equidistante.

Medidas habituales en el ciclismo de montaña son los BCD 104 y BCD 94 y BCD 96 y se presentan con cuatro o cinco orificios.

Cuando el plato tiene cuatro orificios, obtener su BCD es tan sencillo como medir la distancia entre los centros de dos orificios opuestos.

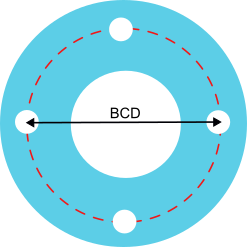
Cuando el plato tenga cinco orificios el proceso será algo más complicado, pero no excesivamente. En este caso tomaremos la medida, en milímetros, de la distancia entre los centros de dos orificios contiguos y realizarremos el siguiente cálculo:

56 x distancia-centros / 32,9.

Por ejemplo, si la medida es de aproximadamente 55 mm (será difícil encontrar el centro exacto del orificio), tendremos: .

56 x 55 / 32,9 = 93,6 que podemos redondear a 94, con lo que el BCD será 94.

Fundamentos matemáticos y método de cálculo para cualquier distribución

Para los que tengan curiosidad acerca de donde sale la fórmula anterior y que además quieran poder calcular el BCD de cualquier distribución regular y circular de tornillos, pernos o sus orificios, no es necesaria más que la aplicación de trigonometría básica.

Sabiendo que la circunferencia tiene 360º, si el plato tiene 5 agujeros equidistantes, el ángulo formado entre dos cualesquiera de esos agujeros será el que resulte de dividir 360 entre 5, es decir, 72º

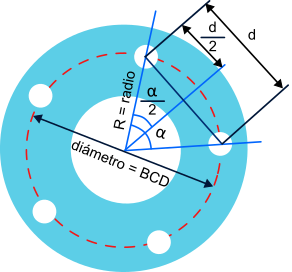
Observando la siguiente figura vemos que podemos obtener todos los elementos necesarios para nuestro cálculo:

Por un lado tenemos el radio de la circunferencia, tomado desde el centro del disco hasta el centro del orificio. Utilizaremos este segmento como hipotenusa del triángulo rectángulo.
Por otro lado tenemos el ángulo alfa formado entre dos orificios. La bisectriz de este ángulo (línea que lo divide en dos partes iguales) definirá el cateto contiguo del triángulo rectángulo y formará un ángulo con la hipotenusa de alfa / 2.
Y finalmente, vemos que la distancia entre centros de los orificios contiguos d queda también dividida por dos por la bisectriz, con lo que ahí tendremos el cateto opuesto que nos faltaba para completar nuestro triángulo rectángulo y su longitud será d / 2.

Con estos datos y sabiendo que, en un triángulo rectángulo, el seno del ángulo no recto es igual al cateto opuesto dividido entre la hipotenusa podremos realizar los cálculos que se muestran:

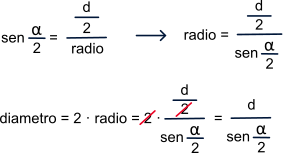
sen ( angulo / 2 ) = (distancia-centros / 2) / radio.

radio = (distancia-centros / 2) / sen ( angulo / 2 ) .

diámetro = 2 · radio .

diámetro = 2 · radio = 2·(distancia-centros / 2) / sen ( angulo / 2 ) = distancia-centros / sen ( angulo / 2 ).

Si suponemos que la medida tomada entre centros ha sido de 55 mm. podemos sustituir "distancia-centros" por esa medida:

Diámetro (BCD) = 55 / sen (36º) = 55 / 0.5878 = 93.57 aprox. 94.

La fórmula rápida que vimos anteriormente (56 x distancia-centros / 32,9 ) está basada en una relación de proporcionalidad derivada de los tamaños más pequeños de anclaje que suelen encontrarse en platos de bicicleta, que son los correspondientes a BCD 56, y con distancia entre agujeros contiguos de 32,9, pero si te fijas el cociente 32,9 / 56 = 0,5878, que es justamente el seno de 36º.

En el caso de que sean seis los orificios, el ángulo entre ellos será de 60º (360º / 6 = 60º) con lo que en nuestros cálculos para seis orificios usaremos el sen(30º) (60º / 2 = 30º), en lugar del de 36º

y el BCD se obtendrá de: BCD = distancia-centros / sen(30)