Power and energy in cycling. A practical calculation.
Power in cycling. Practical calculation
As we saw in the article "Energy, work and power", we can define power as the amount of work or energy use we perform in a given time. It is the speed at which we perform work or use energy.
Therefore, when referring to translational movements, power can be expressed as the product of force multiplied by velocity. In rotational movements we can consider an "instantaneous power" at each pivot point that can be defined as the product of the momentum or torque of the force multiplied by the angular velocity (angle rotated in the unit of time). The angular velocity is equivalent to the pedaling cadence expressed in angle values per second.
Power(w) = Torque (Nm) x Cadence (rad/seg)
The equivalence between revolutions per minute, radians per second and sexagesimal degrees per second is: 1
rpm = 2·PI/60 rad/sec = 360/60 º/sec
Recommended article: Energy, Work and Power, some physical definitions
Energy consumed (Kj): From a graphical point of view, the energy consumed when performing an effort at a certain power corresponds to the area under the power curve. If we refer to the power developed while cycling, running or walking along a route, the total energy consumed would be the total area under the power curve developed along the route.
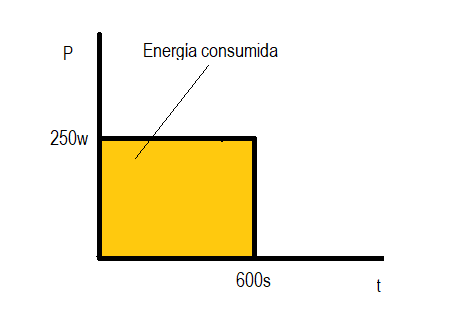
Energy calculation
Example: If we have a cyclist performing a fixed effort of 250 watts for 10 minutes (600 seconds). The entire area under that curve (which is a horizontal line in this case) is the energy expended to produce that power.
Power = (work or energy) / time
clearing up energy in this formula,
Energy = Power x time
and replacing the values,
Energy = 250w x 600 s = 21600 joule = 216 kj
In this case it is evident the coincidence with the area of the rectangle of base time (600 sec) and height power (250 w) because being a constant power its graph is a horizontal line.
Sicami Tracks - Home