BCD or bolt circle diameter of a bicycle chainring
BCD or bolt circle diameter of a bicycle chainring
BCD bicycle chainrings The BCD (Bolt Circle Diameter) or bolt circle diameter of a bicycle transmission chainring is the diameter of the imaginary circle that passes through the center of the bolt holes, provided they are arranged following a circular and equidistant pattern.
Common measurements in mountain biking are BCD 104 and BCD 94 and BCD 96 and they come with four or five holes.
When the chainring has four holes, getting your BCD is as simple as measuring the distance between the centers of two opposite holes.
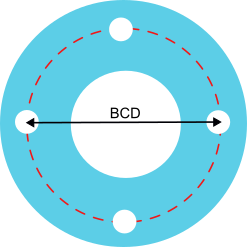
When the plate has five holes, the process will be somewhat more complicated, but not excessively. In this case we will take the measurement, in millimeters, of the distance between the centers of two adjacent holes and we will carry out the following calculation:
56 x distance-centers / 32.9.
For example, if the measurement is approximately 55 mm (it will be difficult to find the exact center of the hole), we will have: .
56 x 55 / 32.9 = 93.6 which we can round to 94, with which the BCD will be 94.
Mathematical foundations and calculation method for any distribution
For those who are curious about where the previous formula comes from and who also want to be able to calculate the BCD of any regular distribution and circular of screws, bolts or their holes, it is not necessary more than the application of basic trigonometry.
Knowing that the circumference has 360º, if the plate has 5 equidistant holes, the angle formed between any two of those holes will be the one that results from dividing 360 by 5, that is, 72º
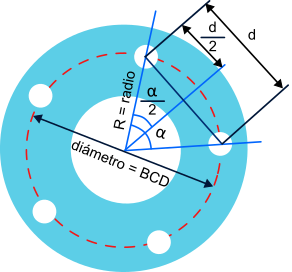
Observing the following figure we see that we can obtain all the necessary elements for our calculation:
On the one hand we have the radius of the circumference, taken from the center of the disc to the center of the hole. We will use this segment as the hypotenuse of the right triangle.
On the other hand we have the angle alpha formed between two holes. The bisector of this angle (line that divides it into two equal parts) will define the contiguous leg of the right triangle and will form an angle with the hypotenuse of alpha / 2.
And finally, we see that the distance between the centers of the adjacent holes d is also divided by two by the bisector, so there we will have the opposite leg that we needed to complete our right triangle and its length will be d / 2.
With these data and knowing that, in a right triangle, the sine of the non-right angle is equal to the opposite leg divided by the hypotenuse, we can perform the calculations shown:
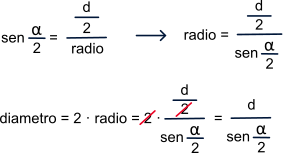
sin ( angle / 2 ) = ( distance-centers / 2) / radius.
radius = (distance-centers / 2) / sin ( angle / 2 ) .
diameter = 2 · radius .
diameter = 2 · radius = 2 · (distance-centres / 2) / sin ( angle / 2 ) = distance-centres / sin ( angle / 2 ).
If we assume that the measurement taken between centers has been 55 mm. we can substitute "distance-centers" for that measure:
Diameter (BCD) = 55 / sin (36º) = 55 / 0.5878 = 93.57 approx. 94.
The quick formula that we saw previously (56 x distance-centers / 32.9 ) is based on a proportional relationship derived from the smallest anchor sizes that are usually found in bicycle chainrings, which are those corresponding to BCD 56, and with distance between adjacent holes of 32.9, but if you look at the quotient 32.9 / 56 = 0.5878, which is precisely the sine of 36º.
In the event that there are six holes, the angle between them will be 60º (360º / 6 = 60º) so in our calculations for six holes we will use sin(30º) (60º / 2 = 30º), instead of the of 36º
and the BCD will be obtained from: BCD = distance-centers / sin(30)
Sicami Tracks - Inizio